Page 47 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp
P. 47
Document Title
Fundamentals of Stress and Vibration 2. Engineering Mechanics Chapter
[A Practical guide for aspiring Designers / Analysts]
ȏ ʹǤ͵ͷȐ ǡ
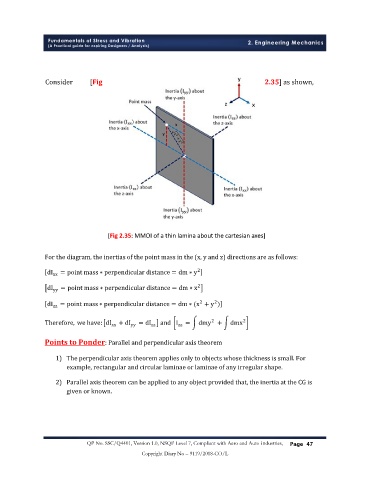
[Fig 2.35: MMOI of a thin lamina about the cartesian axes]
For the diagram, the inertias of the point mass in the (x, y and z) directions are as follows:
2
dI xx = point mass ∗ perpendicular distance = dm ∗ y
2
dI yy = point mass ∗ perpendicular distance = dm ∗ x
2
2
dI zz = point mass ∗ perpendicular distance = dm ∗ (x + y )
2
2
Therefore, we have: dI xx + dI yy = dI and I zz = dmy + dmx
zz
Points to Ponder: Parallel and perpendicular axis theorem
1) The perpendicular axis theorem applies only to objects whose thickness is small. For
example, rectangular and circular laminae or laminae of any irregular shape.
2) Parallel axis theorem can be applied to any object provided that, the inertia at the CG is
given or known.
QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries, P
Page 47 age 47
Copyright Diary No – 9119/2018-CO/L