Page 393 - Color_Atlas_of_Physiology_5th_Ed._-_A._Despopoulos_2003

–
by 0.18 units to pH 6.82. If the initial [A ] /[AH] ratio
had been 3/17, the pH would have dropped from an Concentration
initial pH 6.25 (7 plus the log of 3/17 = 6.25) to pH ratio of
buffer pair
5.7 (7 + log of 1/19 = 5.7), i.e., by 0.55 pH units after [AH]:[A ] –
addition of the same quantity of H ions.
+
10:0
+
The titration of a buffer solution with H (or 9:1
–
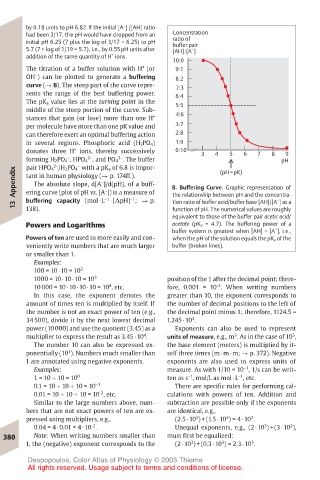
OH ) can be plotted to generate a buffering 8:2
curve (! B). The steep part of the curve repre- 7:3
sents the range of the best buffering power. 6:4
The pK a value lies at the turning point in the 5:5
middle of the steep portion of the curve. Sub-
stances that gain (or lose) more than one H + 4:6
per molecule have more than one pK value and 3:7
can therefore exert an optimal buffering action 2:8
in several regions. Phosphoric acid (H 3PO 4) 1:9
+
donates three H ions, thereby successively 0:10 3 4 5 6 7 8 9
3–
2–
forming H 2PO 4 , HPO 4 , and PO 4 . The buffer pH
–
2–
–
pair HPO 4 /H 2PO 4 with a pK a of 6.8 is impor-
Appendix ering curve (plot of pH vs. [A ]) is a measure of B. Buffering Curve. Graphic representation of
(pH=pK)
tant in human physiology (! p. 174ff.).
The absolute slope, d[A ]/d(pH), of a buff-
–
–
–1
–1
–
tion ratio of buffer acid/buffer base [AH]/[A ] as a
13 buffering capacity (mol · L · [∆pH] ; ! p. the relationship between pH and the concentra-
138).
function of pH. The numerical values are roughly
equivalent to those of the buffer pair acetic acid/
Powers and Logarithms acetate (pK a = 4.7). The buffering power of a
buffer system is greatest when [AH] = [A ], i.e.,
–
Powers of ten are used to more easily and con- when the pH of the solution equals the pK a of the
veniently write numbers that are much larger buffer (broken lines).
or smaller than 1.
Examples:
100 = 10 · 10 = 10 2
1000 = 10 · 10 · 10 = 10 3 position of the 1 after the decimal point; there-
4
-3
10 000 = 10 · 10 · 10 · 10 = 10 , etc. fore, 0.001 = 10 . When writing numbers
In this case, the exponent denotes the greater than 10, the exponent corresponds to
amount of times ten is multiplied by itself. If the number of decimal positions to the left of
the number is not an exact power of ten (e.g., the decimal point minus 1; therefore, 1124.5 =
34 500), divide it by the next lowest decimal 1.245 · 10 . 3
power (10 000) and use the quotient (3.45) as a Exponents can also be used to represent
3
multiplier to express the result as 3.45 · 10 . 4 units of measure, e.g., m . As in the case of 10 , 3
The number 10 can also be expressed ex- the base element (meters) is multiplied by it-
1
ponentially (10 ). Numbers much smaller than self three times (m · m · m; ! p. 372). Negative
1 are annotated using negative exponents. exponents are also used to express units of
–1
Examples: measure. As with 1/10 = 10 , 1/s can be writ-
–1
–1
1 = 10 % 10 = 10 0 ten as s , mol/L as mol · L , etc.
0.1 = 10 % 10 % 10 = 10 –1 There are specific rules for performing cal-
0.01 = 10 % 10 % 10 = 10 , etc. culations with powers of ten. Addition and
-2
Similar to the large numbers above, num- subtraction are possible only if the exponents
bers that are not exact powers of ten are ex- are identical, e.g.,
pressed using multipliers, e.g., (2.5 · 10 ) + (1.5 · 10 ) = 4 · 10 .
2
2
2
-2
2
3
0.04 = 4 · 0.01 = 4 · 10 . Unequal exponents, e.g., (2 · 10 ) + (3 · 10 ),
380 Note: When writing numbers smaller than must first be equalized:
3
3
1, the (negative) exponent corresponds to the (2 · 10 ) + (0.3 · 10 ) = 2.3 · 10 . 3
Despopoulos, Color Atlas of Physiology © 2003 Thieme
All rights reserved. Usage subject to terms and conditions of license.