Page 401 - Buku Materi Pembelajaran Rangkaian Listrik II dan Praktikum

Ruas kiri dan ruas kanan dari persamaan [9.33] sama-sama dikuadratkan
yang menghasilkan persamaan [9.66].

1
2
2
4π (f ) = LC [9.66]
0

Persamaan [9.66] dapat dinyatakan sebagaimana persamaan [9.67] untuk
menentukan nilai kapasitansi C.
1
C = [9.67]
2
2
4π (f 0 ) L

Nilai kapasitansi C berdasarkan persamaan [9.67] adalah sebagai berikut:

1 1
C = = = 0,102 µF
4 2
2
2
2
4π (f ) L 4π x(10 ) x2,5x10 −3
0

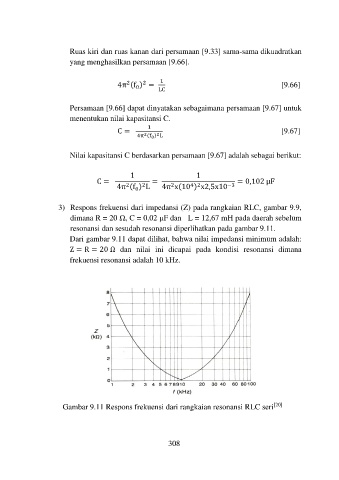
3) Respons frekuensi dari impedansi (Z) pada rangkaian RLC, gambar 9.9,
dimana R = 20 Ω, C = 0,02 μF dan L = 12,67 mH pada daerah sebelum
resonansi dan sesudah resonansi diperlihatkan pada gambar 9.11.
Dari gambar 9.11 dapat dilihat, bahwa nilai impedansi minimum adalah:
Z = R = 20 Ω dan nilai ini dicapai pada kondisi resonansi dimana
frekuensi resonansi adalah 10 kHz.

Ga mbar 9.11 Respons frekuensi dari rangkaian resonansi RLC seri [20]

.

308