Page 25 - Focus SPM KSSM Tg 4.5 - Add Maths

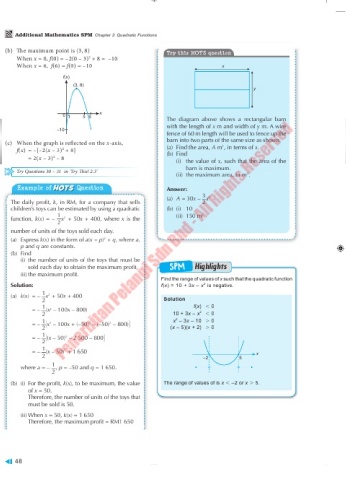
Additional Mathematics SPM Chapter 2 Quadratic Functions

(b) The maximum point is (3, 8) Try this HOTS question
When x = 0, f(0) = –2(0 – 3) + 8 = –10
2
When x = 6, f(6) = f(0) = –10 x
f(x)
(3, 8)
y

x
0 1 5 6
The diagram above shows a rectangular barn
with the length of x m and width of y m. A wire
–10
fence of 60 m length will be used to fence up the
(c) When the graph is reflected on the x-axis, barn into two parts of the same size as shown.
2
f(x) = –[–2(x – 3) + 8] (a) Find the area, A m , in terms of x.
2
Form 4
= 2(x – 3) – 8 (b) Find
2
(i) the value of x, such that the area of the
barn is maximum.
Try Questions 30 – 31 in ‘Try This! 2.3’
(ii) the maximum area, in m .
2
Example of HOTS Answer:
HOTS Question
3 2
(a) A = 30x – x
The daily profit, k, in RM, for a company that sells 2
children’s toys can be estimated by using a quadratic (b) (i) 10
1 (ii) 150 m 2
function, k(x) = – x + 50x + 400, where x is the
2
2
number of units of the toys sold each day.
2
(a) Express k(x) in the form of a(x + p) + q, where a,
p and q are constants.
(b) Find
(i) the number of units of the toys that must be
sold each day to obtain the maximum profit, SPM Highlights
(ii) the maximum profit.
Find the range of values of x such that the quadratic function
2
Solution: f(x) = 10 + 3x – x is negative.
(a) k(x) = – x + 50x + 400
1 2
2 Solution
1 f(x)  0
= – (x – 100x – 800) 2
2
2 10 + 3x – x  0
2
1
= – x – 100x + (–50) – (–50) – 800) x – 3x – 10 . 0
2
2
2
2 (x – 5)(x + 2) . 0
1
= – (x – 50) – 2 500 – 800
2
2
1
= – (x – 50) + 1 650
2
2 –2 5 x
1
where a = – , p = –50 and q = 1 650.
2
(b) (i) For the profit, k(x), to be maximum, the value The range of values of is x  –2 or x . 5.
of x = 50.
Therefore, the number of units of the toys that
must be sold is 50.
(ii) When x = 50, k(x) = 1 650
Therefore, the maximum profit = RM1 650
48