Page 11 - TOP ONE ADDMATHS TG4

Additional Mathematics Form 4 Chapter 2 Quadratic Functions

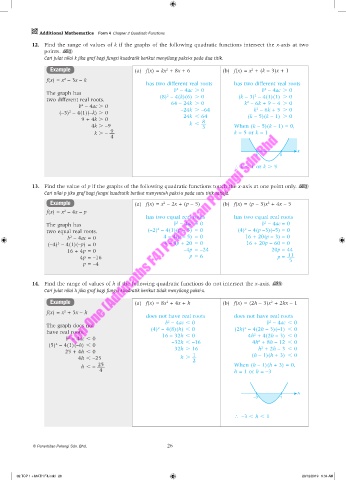
12. Find the range of values of k if the graphs of the following quadratic functions intersect the x-axis at two
points. PL 3
Cari julat nilai k jika graf bagi fungsi kuadratik berikut menyilang paksi-x pada dua titik.
Example (a) f(x) = kx + 8x + 6 (b) f(x) = x + (k – 3)x + 1
2
2
f(x) = x – 3x – k
2
has two different real roots has two different real roots
b – 4ac . 0 b – 4ac . 0
2
2
The graph has (8) – 4(k)(6) . 0 (k – 3) – 4(1)(1) . 0
2
2
two different real roots. 64 – 24k . 0 k – 6k + 9 – 4 . 0
2
2
b – 4ac . 0 2
k – 6k + 5 . 0
(–3) – 4(1)(–k) . 0 –24k . –64 (k – 5)(k – 1) . 0
2
24k , 64
9 + 4k . 0 8
4k . –9 k , 3 When (k – 5)(k – 1) = 0,
k . – 9 k = 5 or k = 1
4
k
1 5
∴ k , 1 or k . 5
13. Find the value of p if the graphs of the following quadratic functions touch the x-axis at one point only. PL 3
Cari nilai p jika graf bagi fungsi kuadratik berikut menyentuh paksi-x pada satu titik sahaja.
Example (a) f(x) = x – 2x + (p – 5) (b) f(x) = (p – 3)x + 4x – 5
2
2
f(x) = x – 4x – p
2
has two equal real roots has two equal real roots
2
2
The graph has b – 4ac = 0 b – 4ac = 0
2
2
two equal real roots. (–2) – 4(1)(p – 5) = 0 (4) – 4(p –3)(–5) = 0
2
b – 4ac = 0 4 – 4(p – 5) = 0 16 + 20(p – 3) = 0
2
(–4) – 4(1)(–p) = 0 4 – 4p + 20 = 0 16 + 20p – 60 = 0
16 + 4p = 0 –4p = –24 20p = 44
4p = –16 p = 6 p = 11
5
p = –4
14. Find the range of values of h if the following quadratic functions do not intersect the x-axis. PL 3
Cari julat nilai h jika graf bagi fungsi kuadratik berikut tidak menyilang paksi-x.
Example (a) f(x) = 8x + 4x + h (b) f(x) = (2h – 3)x + 2hx – 1
2
2
2
f(x) = x + 5x – h
does not have real roots does not have real roots
b – 4ac , 0 b – 4ac , 0
2
2
The graph does not 2 2
have real roots. (4) – 4(8)(h) , 0 (2h) – 4(2h – 3)(–1) , 0
2
b – 4ac , 0 16 – 32h , 0 4h + 4(2h – 3) , 0
2
2
(5) – 4(1)(–h) , 0 –32h , –16 4h + 8h – 12 , 0
2
2
25 + 4h , 0 32h . 16 h + 2h – 3 , 0
4h , –25 h . 1 (h – 1)(h + 3) , 0
2
h , – 25 When (h – 1)(h + 3) = 0,
4 h = 1 or h = –3
h
–3 1

∴ –3 , h , 1

© Penerbitan Pelangi Sdn. Bhd. 26

02 TOP 1 + MATH F4.indd 26 20/12/2019 9:34 AM