Page 14 - TOP ONE ADDMATHS TG4

Additional Mathematics Form 4 Chapter 2 Quadratic Functions

17. Sketch the graph of each of the following quadratic functions. PL 4
Lakarkan graf bagi setiap fungsi kuadratik berikut.

Example
2
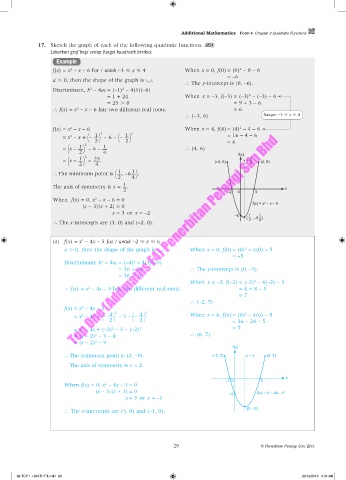
f(x) = x – x – 6 for / untuk –3 < x < 4 When x = 0, f(0) = (0) – 0 – 6
2
= –6
a . 0, then the shape of the graph is .
∴ The y-intercept is (0, –6).
2
2
Discriminant, b – 4ac = (–1) – 4(1)(–6)
2
= 1 + 24 When x = –3, f(–3) = (–3) – (–3) – 6
= 25 . 0 = 9 + 3 – 6
2
∴ f(x) = x – x – 6 has two different real roots. = 6
∴ (−3, 6) Range: –3 < x < 4
f(x) = x – x – 6 When x = 4, f(4) = (4) – 4 – 6
2
2


2
= x – x + – 1  2 – 6 – – 1  2 = 16 – 4 – 6
2
2
= 6

= x – 1  2 – 6 – 1 ∴ (4, 6) f(x)
2
4

= x – 1  2 – 25 (–3, 6) x = 1 2 (4, 6)
2 4
∴ The minimum point is  1 , –6 1  .
2
4
1
The axis of symmetry is x = .
2 –2 0 3 x
When f(x) = 0, x – x – 6 = 0 2
2
(x – 3)(x + 2) = 0 f(x) = x – x – 6
= 3 or x = –2
–6 1 1
( , –6 )
∴ The x-intercepts are (3, 0) and (–2, 0). 2 4
(a) f(x) = x – 4x – 5 for / untuk –2 < x < 6
2
a . 0, then the shape of the graph is . When x = 0, f(0) = (0) – 4(0) – 5
2
= –5
2
2
Discriminant, b – 4ac = (–4) – 4(1)(–5)
= 16 + 20 ∴ The y-intercept is (0, –5).
= 36 . 0
When x = –2, f(–2) = (–2) – 4(–2) – 5
2
2
∴ f(x) = x – 4x – 5 has two different real roots. = 4 + 8 – 5
= 7
∴ (–2, 7)
2
f(x) = x – 4x – 5


2
= x – 4x + – 4  2 – 5 – – 4  2 When x = 6, f(6) = (6) – 4(6) – 5
2
2
2
= 36 – 24 – 5

2
2
= x – 4x + (–2) – 5 – (–2) 2 = 7
2
= (x – 2) – 5 – 4 ∴ (6, 7)
2
= (x – 2) – 9
f(x)
∴ The minimum point is (2, –9). (–2, 7) x = 2 (6, 7)
The axis of symmetry is x = 2.
x
–1 0 5
2
When f(x) = 0, x – 4x – 5 = 0
(x – 5)(x + 1) = 0 –5 f(x) = x – 4x – 5
2
x = 5 or x = –1

∴ The x-intercepts are (5, 0) and (–1, 0). (2, –9)
29 © Penerbitan Pelangi Sdn. Bhd.
02 TOP 1 + MATH F4.indd 29 20/12/2019 9:34 AM