Page 12 - TOP ONE ADDMATHS TG4

Additional Mathematics Form 4 Chapter 2 Quadratic Functions

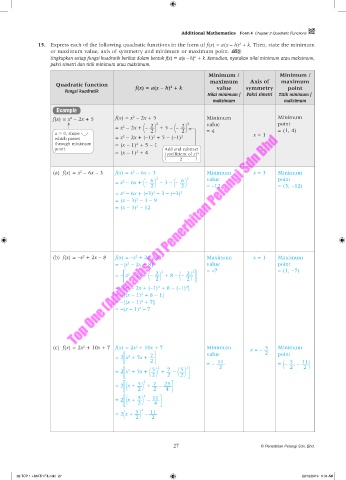
15. Express each of the following quadratic functions in the form of f(x) = a(x – h) + k. Then, state the minimum
2
or maximum value, axis of symmetry and minimum or maximum point. PL 3
2
Ungkapkan setiap fungsi kuadratik berikut dalam bentuk f(x) = a(x – h) + k. Kemudian, nyatakan nilai minimum atau maksimum,
paksi simetri dan titik minimum atau maksimum.
Minimum / Minimum /
maximum Axis of maximum
Quadratic function f(x) = a(x – h) + k value symmetry point
2
Fungsi kuadratik
Nilai minimum / Paksi simetri Titik minimum /
maksimum maksimum
Example
2
f(x) = x – 2x + 5 f(x) = x – 2x + 5 Minimum Minimum
2


= x – 2x + – 2  2 + 5 – – 2  2 value point
2
= (1, 4)
a . 0, shape 2 2 = 4 x = 1
2
2
which passes = x – 2x + (–1) + 5 – (–1) 2
through minimum = (x – 1) + 5 – 1
2
point Add and subtract
= (x – 1) + 4 2
2
 coefficient of x 
2
(a) f(x) = x – 6x – 3 f(x) = x – 6x – 3 Minimum x = 3 Minimum
2
2


2
= x – 6x + – 6  2 – 3 – – 6  2 value point
2
2
= –12
= (3, −12)
= x – 6x + (–3) – 3 – (–3) 2
2
2
2
= (x – 3) – 3 – 9
2
= (x – 3) – 12
2
2
(b) f(x) = –x + 2x – 8 f(x) = –x + 2x – 8 Maximum x = 1 Maximum
= –[x – 2x + 8] value point
2

2
2



= – x – 2x + – 2  2 + 8 – – 2  = –7 = (1, −7)
2
2
2
= –[x – 2x + (–1) + 8 – (–1) ]
2
2
= –[(x – 1) + 8 – 1]
2
2
= –[(x – 1) + 7]
= –(x – 1) – 7
2
2
2
(c) f(x) = 2x + 10x + 7 f(x) = 2x + 10x + 7 Minimum x = – 5 Minimum

7
= 2 x + 5x + 2 value 11 2 point 5 11 
2

= –
= – , –
2 

5
5
7
= 2 x + 5x +   2 + –   2 2 2 2
2
2
2

4 
7

= 2 x + 5  2 + – 25
2
2

4 

= 2 x + 5  2 – 11
2

= 2 x + 5  2 – 11
2
2
27 © Penerbitan Pelangi Sdn. Bhd.
02 TOP 1 + MATH F4.indd 27 20/12/2019 9:34 AM