Page 15 - TOP ONE ADDMATHS TG4

Additional Mathematics Form 4 Chapter 2 Quadratic Functions

2
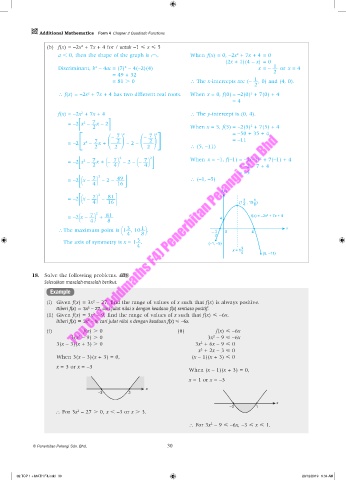
(b) f(x) = –2x + 7x + 4 for / untuk –1 < x < 5
2
a , 0, then the shape of the graph is . When f(x) = 0, –2x + 7x + 4 = 0
(2x + 1)(4 – x) = 0
1
Discriminant, b – 4ac = (7) – 4(–2)(4) x = – or x = 4
2
2
2
= 49 + 32
1
= 81 . 0 ∴ The x-intercepts are (– , 0) and (4, 0).
2
2
∴ f(x) = –2x + 7x + 4 has two different real roots. When x = 0, f(0) = –2(0) + 7(0) + 4
2
= 4

f(x) = –2x + 7x + 4 ∴ The y-intercept is (0, 4).
2

7
2
= –2 x – x – 2  When x = 5, f(5) = –2(5) + 7(5) + 4
2
2
2
= –2x – x +   2 – 2 –   = –50 + 35 + 4
7
7
–
–
= –11
2
2
7
2
2 2 2 ∴ (5, –11)
= –2 x – x + – 7 2 – 2 – – 4  When x = –1, f(–1) = –2(–1) + 7(–1) + 4

2
7
2
7


 
2
4
2

= –2 – 7 + 4
= –5

49

= –2 x – 7  2 – 2 – 16 ∴ (–1, –5)
4
f(x)

81

= –2 x – 7  2 – 16 (1 , 10 )
3
1
4
8
4

2
= –2 x – 7  2 + 81 4 f(x) = –2x + 7x + 4
8
4

3

∴ The maximum point is 1 , 10 1  . – 1 2 0 4 x
4
8
3
The axis of symmetry is x = 1 . (–1, –5)
4
x = 1 3
4 (5, –11)
18. Solve the following problems. PL 5
Selesaikan masalah-masalah berikut.
Example
2
(i) Given f(x) = 3x – 27, find the range of values of x such that f(x) is always positive.
Diberi f(x) = 3x – 27, cari julat nilai x dengan keadaan f(x) sentiasa positif.
2
(ii) Given f(x) = 3x – 9, find the range of values of x such that f(x) < –6x.
2
2
Diberi f(x) = 3x – 9, cari julat nilai x dengan keadaan f(x) < –6x.
(i) f(x) . 0 (ii) f(x) < –6x
3(x – 9) . 0 3x – 9 < –6x
2
2
2
3(x – 3)(x + 3) . 0 3x + 6x – 9 < 0
x + 2x – 3 < 0
2
When 3(x – 3)(x + 3) = 0, (x – 1)(x + 3) < 0
x = 3 or x = –3
When (x – 1)(x + 3) = 0,
x = 1 or x = –3
x
–3 3
x
–3 1
∴ For 3x – 27 . 0, x , –3 or x . 3.
2
2
∴ For 3x – 9 < –6x, –3 < x < 1.
© Penerbitan Pelangi Sdn. Bhd. 30
02 TOP 1 + MATH F4.indd 30 20/12/2019 9:34 AM