Page 6 - Hybrid PBD 2022 Form 4 Additional Mathematics

BAB
3 Sistem Persamaan
Systems of Equations
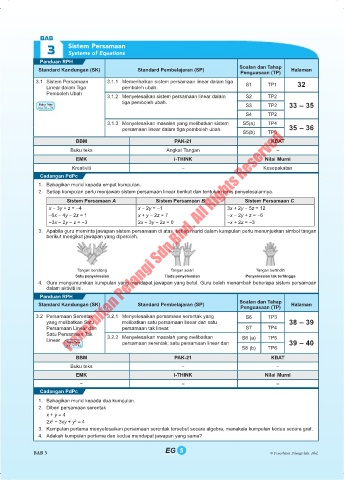
Panduan RPH
Soalan dan Tahap
Standard Kandungan (SK) Standard Pembelajaran (SP) Halaman
Penguasaan (TP)
3.1 Sistem Persamaan 3.1.1 Memerihalkan sistem persamaan linear dalam tiga 32
Linear dalam Tiga pemboleh ubah. S1 TP1
Pemboleh Ubah
3.1.2 Menyelesaikan sistem persamaan linear dalam S2 TP2
tiga pemboleh ubah.
Buku Teks S3 TP2 33 – 35
m.s 70 – 78
S4 TP2
3.1.3 Menyelesaikan masalah yang melibatkan sistem S5(a) TP4
Penerbitan Pelangi Sdn Bhd. All Rights Reserved
persamaan linear dalam tiga pemboleh ubah. 35 – 36
S5(b) TP5
BBM PAK-21 KBAT
Buku teks Angkat Tangan –
EMK i-THINK Nilai Murni
Kreativiti – Kesepakatan
Cadangan PdPc
1. Bahagikan murid kepada empat kumpulan.
2. Setiap kumpulan perlu menjawab sistem persamaan linear berikut dan tentukan jenis penyelesaiannya.
Sistem Persamaan A Sistem Persamaan B Sistem Persamaan C
x − 3y + z = −4 x − 2y = −1 3x + 2y − 5z = 12
–6x − 4y − 2z = 1 x + y − 2z = 7 −x − 2y + z = −6
−3x − 2y − z = −3 2x − 3y − 2z = 0 −x + 2z = −3
3. Apabila guru meminta jawapan sistem persamaan di atas, setiap murid dalam kumpulan perlu menunjukkan simbol tangan
berikut mengikut jawapan yang diperoleh.

Tangan bersilang Tangan selari Tangan bertindih
Satu penyelesaian Tiada penyelesaian Penyelesaian tak terhingga
4. Guru mengumumkan kumpulan yang mendapat jawapan yang betul. Guru boleh menambah beberapa sistem persamaan
dalam aktiviti ini.
Panduan RPH
Soalan dan Tahap
Standard Kandungan (SK) Standard Pembelajaran (SP) Halaman
Penguasaan (TP)
3.2 Persamaan Serentak 3.2.1 Menyelesaikan persamaan serentak yang S6 TP3
yang melibatkan Satu melibatkan satu persamaan linear dan satu 38 – 39
Persamaan Linear dan persamaan tak linear. S7 TP4
Satu Persamaan Tak
Linear 3.2.2 Menyelesaikan masalah yang melibatkan S8 (a) TP5
Buku Teks persamaan serentak; satu persamaan linear dan 39 – 40
m.s 79 – 84
S8 (b) TP6
BBM PAK-21 KBAT
Buku teks – –
EMK i-THINK Nilai Murni
– – –
Cadangan PdPc
1. Bahagikan murid kepada dua kumpulan.
2. Diberi persamaan serentak
x + y = 4
2x − 3xy + y = 4
2
2
3. Kumpulan pertama menyelesaikan persamaan serentak tersebut secara algebra, manakala kumpulan kedua secara graf.
4. Adakah kumpulan pertama dan kedua mendapat jawapan yang sama?

BAB 3 EG 5 © Penerbitan Pelangi Sdn. Bhd.

00 Strategi PdPc MT Tg4.indd 5 30/09/2021 11:22 AM