Page 10 - PBD Plus Matematik T5 (EG)

Matematik Tingkatan 5 Bab 1 Ubahan
SP 1.1.2 Menentukan hubungan antara dua pemboleh ubah bagi suatu ubahan langsung.

2. Selesaikan. TP 2
Solve.
Contoh
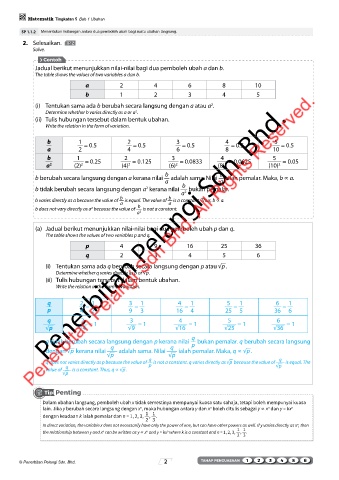
Jadual berikut menunjukkan nilai-nilai bagi dua pemboleh ubah a dan b.
The table shows the values of two variables a dan b.
a 2 4 6 8 10
b 1 2 3 4 5
(i) Tentukan sama ada b berubah secara langsung dengan a atau a .
Penerbitan Pelangi Sdn. Bhd.
2
Determine whether b varies directly as a or a .
2
(ii) Tulis hubungan tersebut dalam bentuk ubahan.
Write the relation in the form of variation.
b 1 = 0.5 2 = 0.5 3 = 0.5 4 = 0.5 5 = 0.5
a 2 4 6 8 10
b 1 = 0.25 2 = 0.125 3 = 0.0833 4 = 0.0625 5 = 0.05
a 2 (2) 2 (4) 2 (6) 2 (8) 2 (10) 2
b b
b berubah secara langsung dengan a kerana nilai adalah sama. Nilai ialah pemalar. Maka, b ∝ a.
a a
2
b tidak berubah secara langsung dengan a kerana nilai a b 2 bukan pemalar.
b b
b varies directly as a because the value of is equal. The value of is a constant. Thus, b ∝ a.
a a
b does not vary directly as a because the value of b is not a constant.
2
a 2
(a) Jadual berikut menunjukkan nilai-nilai bagi dua pemboleh ubah p dan q.
The table shows the values of two variables p and q.
p 4 9 16 25 36
q 2 3 4 5 6

(i) Tentukan sama ada q berubah secara langsung dengan p atau √p .
Determine whether q varies directly as p or √p .
(ii) Tulis hubungan tersebut dalam bentuk ubahan.
Write the relation in the form of variation.

q 2 = 1 3 = 1 4 = 1 5 = 1 6 = 1
p 4 2 9 3 16 4 25 5 36 6
q 2 3 4 5 6
√p √4 = 1 √9 = 1 √16 = 1 √25 = 1 √36 = 1
q
q tidak berubah secara langsung dengan p kerana nilai bukan pemalar. q berubah secara langsung
q q p
dengan √p kerana nilai adalah sama. Nilai ialah pemalar. Maka, q ∝ √p .
√p √p
q
q does not varies directly as p because the value of is not a constant. q varies directly as √p because the value of q is equal. The
p
value of q is a constant. Thus, q ∝ √p . √p
√p

Tip penting

Dalam ubahan langsung, pemboleh ubah x tidak semestinya mempunyai kuasa satu sahaja, tetapi boleh mempunyai kuasa
n
lain. Jika y berubah secara langsung dengan x , maka hubungan antara y dan x boleh ditulis sebagai y ∝ x dan y = kx
n
n
n
1 1
dengan keadaan k ialah pemalar dan n = 1, 2, 3, , .
2 3
n
In direct variation, the variable x does not necessarily have only the power of one, but can have other powers as well. If y varies directly as x , then
1 1
the relationship between y and x can be written as y ∝ x and y = kx where k is a constant and n = 1, 2, 3, , .
n
n
n
2 3
© Penerbitan Pelangi Sdn. Bhd. 2 Tahap penguasaan 1 2 3 4 5 6