Page 201 - Learn To Program With Scratch

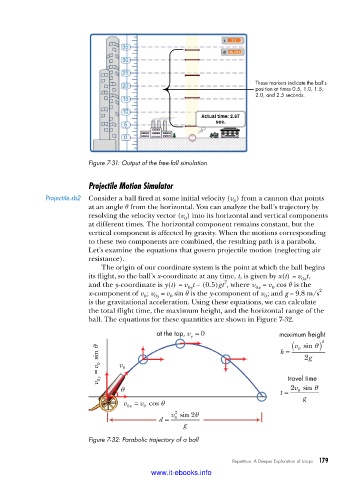
These markers indicate the ball’s
position at times 0.5, 1.0, 1.5,
2.0, and 2.5 seconds.

Figure 7-31: Output of the free-fall simulation

Projectile Motion Simulator

Projectile .sb2 Consider a ball fired at some initial velocity (v ) from a cannon that points
0
at an angle q from the horizontal. You can analyze the ball’s trajectory by
resolving the velocity vector (v ) into its horizontal and vertical components
0
at different times. The horizontal component remains constant, but the
vertical component is affected by gravity. When the motions corresponding
to these two components are combined, the resulting path is a parabola.
Let’s examine the equations that govern projectile motion (neglecting air
resistance).
The origin of our coordinate system is the point at which the ball begins
its flight, so the ball’s x-coordinate at any time, t, is given by x(t) = v t,
0x
2
and the y-coordinate is y(t) = v t − (0.5)gt , where v = v cos q is the
0y
0x
0
2
x- component of v ; v = v sin q is the y-component of v ; and g = 9.8 m/s
0
0
0y
0
is the gravitational acceleration. Using these equations, we can calculate
the total flight time, the maximum height, and the horizontal range of the
ball. The equations for these quantities are shown in Figure 7-32.
at the top, v = 0 maximum height
y
v (
2
v 0 sin θ v h = sin θ ) 0
2
g
= 0
y travel time
v 0
θ t = v 2 sin θ
0
v 0 x = v cos θ g
0
2
v sin 2θ
d = 0
g
Figure 7-32: Parabolic trajectory of a ball
Repetition: A Deeper Exploration of Loops 179
www.it-ebooks.info