Page 172 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

148 MÉTODOS ABIERTOS

FUNCTION Fixpt(x0, es, imax iter, ea)
xr = x0
iter = 0
DO
xrold = xr
xr = g(xrold)
iter = iter + 1
lF xr ≠ 0 THEN
xr– xrold
ea = ⋅ 100
FIGURA 6.4 xr
Seudocódigo para el mé- END IF
todo de punto fi jo. Note IF ea < es 0R iter ≥ imax EXIT
que otros métodos abiertos END DO
pueden diseñarse en este Fixpt = xr
formato general. END Fixpt

f(x)

Pendiente = f'(x )
i
f(x )
i

f(x ) –0
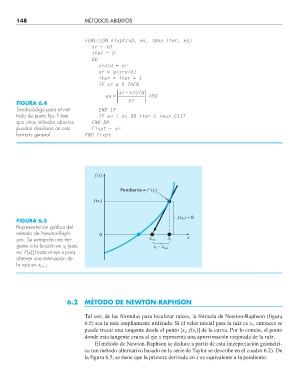
FIGURA 6.5 i
Representación gráfi ca del
método de Newton-Raph- 0
son. Se extrapola una tan- x i+1 x i x
gente a la función en x i [esto x – x i+1
i
es, f’(x i )] hasta el eje x para
obtener una estimación de
la raíz en x i + 1 .

6.2 MÉTODO DE NEWTON-RAPHSON

Tal vez, de las fórmulas para localizar raíces, la fórmula de Newton-Raphson (figura
6.5) sea la más ampliamente utilizada. Si el valor inicial para la raíz es x , entonces se
i
puede trazar una tangente desde el punto [x , f(x )] de la curva. Por lo común, el punto
i
i
donde esta tangente cruza al eje x representa una aproximación mejorada de la raíz.
El método de Newton-Raphson se deduce a partir de esta interpretación geométri-
ca (un método alternativo basado en la serie de Taylor se describe en el cuadro 6.2). De
la figura 6.5, se tiene que la primera derivada en x es equivalente a la pendiente:

6/12/06 13:49:49
Chapra-06.indd 148 6/12/06 13:49:49
Chapra-06.indd 148