Page 170 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

146 MÉTODOS ABIERTOS

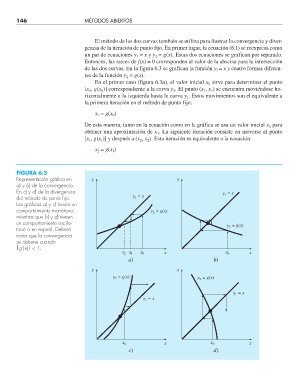
El método de las dos curvas también se utiliza para ilustrar la convergencia y diver-
gencia de la iteración de punto fijo. En primer lugar, la ecuación (6.1) se reexpresa como
un par de ecuaciones y = x y y = g(x). Estas dos ecuaciones se grafican por separado.
1
2
Entonces, las raíces de f(x) = 0 corresponden al valor de la abscisa para la intersección
de las dos curvas. En la figura 6.3 se grafican la función y = x y cuatro formas diferen-
l
tes de la función y = g(x).
2
En el primer caso (figura 6.3a), el valor inicial x sirve para determinar el punto
0
[x , g(x )] correspondiente a la curva y . El punto (x , x ) se encuentra moviéndose ho-
1
0
2
0
1
rizontalmente a la izquierda hasta la curva y . Estos movimientos son el equivalente a
1
la primera iteración en el método de punto fijo:
= g(x )
x 1 0
De esta manera, tanto en la ecuación como en la gráfica se usa un valor inicial x para
0
obtener una aproximación de x . La siguiente iteración consiste en moverse al punto
1
[x , g(x )] y después a (x , x ). Esta iteración es equivalente a la ecuación:
2
2
1
1
x = g(x )
1
2
FIGURA 6.3
Representación gráfi ca en y y
a) y b) de la convergencia.
En c) y d) de la divergencia y = x
1
del método de punto fi jo. y = x
1
Las gráfi cas a) y c) tienen un
comportamiento monótono; y = g(x)
2
mientras que b) y d) tienen
un comportamiento oscila-
y = g(x)
torio o en espiral. Deberá 2
notar que la convergencia
se obtiene cuando
⎪g’(x)⎪ < 1.
x 2 x 1 x 0 x x 0 x
a) b)
y y
y = g(x) y = g(x)
2
2
y = x
1
y = x
1

x x x
x 0 0
c) d)

6/12/06 13:49:49
Chapra-06.indd 146 6/12/06 13:49:49
Chapra-06.indd 146