Page 253 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT2.6 MÉTODOS AVANZADOS Y REFERENCIAS ADICIONALES 229

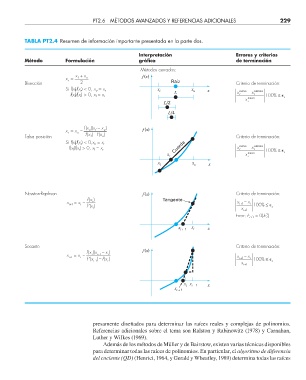
TABLA PT2.4 Resumen de información importante presentada en la parte dos.

Interpretación Errores y criterios
Método Formulación gráfi ca de terminación
Métodos cerrados:
x + x
x = l u f(x)
r
Bisección 2 Raíz Criterio de terminación:
x x
Si f(x l )f(x r ) < 0, x u = x r l u x nuevo anterior
f(x l )f(x r ) > 0, x l = x r L x r – x r 100 % ≤ s
nuevo
x r
L/2
L/4
fx x()( – x )
x = x – u l u f(x)
r
u
Falsa posición fx() – fx( ) Criterio de terminación:
u
l
Si f(x l )f(x r ) < 0,x u = x r
f(x l )f(x r ) > 0, x l = x r Cuerda x nuevo – x r anterior 100 % ≤ s
r
x r x r nuevo
x l x u x
Métodos abiertos:
Newton-Raphson f(x) Criterio de terminación:
fx() Tangente
x + = x – i x +1 – x i 100% ≤
i
i 1
i
fx ′() i x +1 s
i
Error: E i+1 = 0(E i ) 2
x i + 1 x i x
Secante Criterio de terminación:
()( – x ) f(x)
x + = x – fx x −1 i
i
i
i 1 i x i+1 – x i
′(
fx −1 ) – f x( ) i x i+1 100% ≤ s
i
x x i – 1 x
i
x i + 1

presamente diseñados para determinar las raíces reales y complejas de polinomios.
Referencias adicionales sobre el tema son Ralston y Rabinowitz (1978) y Carnahan,
Luther y Wilkes (1969).
Además de los métodos de Müller y de Bairstow, existen varias técnicas disponibles
para determinar todas las raíces de polinomios. En particular, el algoritmo de diferencia
del cociente (QD) (Henrici, 1964, y Gerald y Wheatley, 1989) determina todas las raíces

6/12/06 13:52:01
Chapra-08.indd 229 6/12/06 13:52:01
Chapra-08.indd 229