Page 444 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

420 OPTIMIZACIÓN RESTRINGIDA

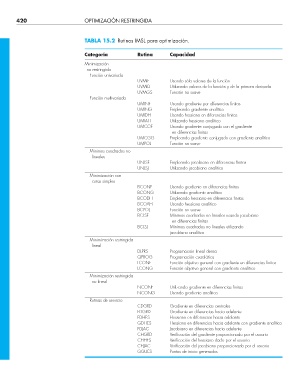
TABLA 15.2 Rutinas IMSL para optimización.

Categoría Rutina Capacidad
Minimización
no restringida
Función univariada
UVMIF Usando sólo valores de la función
UVMID Utilizando valores de la función y de la primera derivada
UVMGS Función no suave
Función multivariada
UMINF Usando gradiente por diferencias fi nitas
UMING Empleando gradiente analítico
UMIDH Usando hessiano en diferencias fi nitas
UMIAH Utilizando hessiano analítico
UMCGF Usando gradiente conjugado con el gradiente
en diferencias fi nitas
UMCGG Empleando gradiente conjugado con gradiente analítico
UMPOL Función no suave
Mínimos cuadrados no
lineales
UNLSF Empleando jacobiano en diferencias fi nitas
UNLSJ Utilizando jacobiano analítico
Minimización con
cotas simples
BCONF Usando gradiente en diferencias fi nitas
BCONG Utilizando gradiente analítico
BCODH Empleando hessiano en diferencias fi nitas
BCOAH Usando hessiano analítico
BCPOL Función no suave
BCLSF Mínimos cuadrados no lineales usando jacobiano
en diferencias fi nitas
BCLSJ Mínimos cuadrados no lineales utilizando
jacobiano analítico
Minimización restringida
lineal
DLPRS Programación lineal densa
QPROG Programación cuadrática
LCONF Función objetivo general con gradiente en diferencias fi nitas
LCONG Función objetivo general con gradiente analítico
Minimización restringida
no lineal
NCONF Utilizando gradiente en diferencias fi nitas
NCONG Usando gradiente analítico
Rutinas de servicio
CDGRD Gradiente en diferencias centrales
FDGRD Gradiente en diferencias hacia adelante
FDHES Hessiano en diferencias hacia adelante
GDHES Hessiano en diferencias hacia adelante con gradiente analítico
FDJAC Jacobiano en diferencias hacia adelante
CHGRD Verifi cación del gradiente proporcionado por el usuario
CHHES Verifi cación del hessiano dado por el usuario
CHJAC Verifi cación del jacobiano proporcionado por el usuario
GGUES Puntos de inicio generados

6/12/06 13:56:07
Chapra-15.indd 420 6/12/06 13:56:07
Chapra-15.indd 420