Page 603 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

20.1 REGRESIÓN LINEAL Y MODELOS DE POBLACIÓN 579

tóxicos. Una manera de expresar esto en forma matemática es mediante el uso de un
modelo de velocidad de crecimiento de saturación tal que
f
k = k máx = K + f (20.3)

donde k máx = la velocidad de crecimiento máximo obtenible para valores grandes de
alimento (f) y K = la constante de saturación media. En la figura 20.1 se tiene la gráfi-
ca de la ecuación (20.3) y se muestra que cuando f = K, k = k máx /2. Por lo tanto, K es la
cantidad de alimento disponible que permite una velocidad de crecimiento poblacional
igual a la mitad de la velocidad máxima.
son valores empíricos obtenidos de mediciones experimen-
Las constantes K y k máx
tales de k para diversos valores de f. Por ejemplo, suponga que la población p representa
la levadura empleada en la producción comercial de cerveza, y f es la concentración de
la fuente de carbono que será fermentada. Las mediciones de k contra f para la levadura
se muestran en la tabla 20.1.

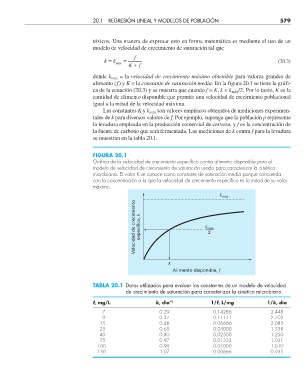
FIGURA 20.1
Gráfi ca de la velocidad de crecimiento específi co contra alimento disponible para el
modelo de velocidad de crecimiento de saturación usado para caracterizar la cinética
microbiana. El valor K se conoce como constante de saturación media porque concuerda
con la concentración a la que la velocidad de crecimiento específi co es la mitad de su valor
máximo.
k máx
Velocidad de crecimiento específico, k k máx

2

K
Alimento disponible, f

TABLA 20.1 Datos utilizados para evaluar las constantes de un modelo de velocidad
de crecimiento de saturación para caracterizar la cinética microbiana.

f, mg/L k, día –1 1/f, L/mg 1/k, día
7 0.29 0.14286 3.448
9 0.37 0.11111 2.703
15 0.48 0.06666 2.083
25 0.65 0.04000 1.538
40 0.80 0.02500 1.250
75 0.97 0.01333 1.031
100 0.99 0.01000 1.010
150 1.07 0.00666 0.935

6/12/06 13:58:56
Chapra-20.indd 579 6/12/06 13:58:56
Chapra-20.indd 579