Page 605 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

20.1 REGRESIÓN LINEAL Y MODELOS DE POBLACIÓN 581

k máx

1
k, día –1

0 50 100 150
f, mg/L

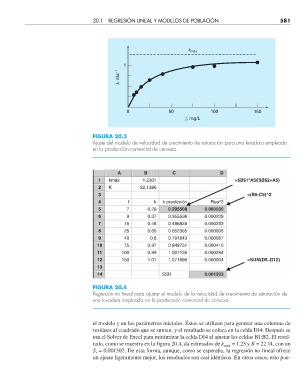
FIGURA 20.3
Ajuste del modelo de velocidad de crecimiento de saturación para una levadura empleada
en la producción comercial de cerveza.

A B C D
1 kmáx 1.2301 =$B$1*A5/($B$2+A5)
2 K 22.1386
3 =(B5-C5)^2
4 f k k-predicción Res^2
5 7 0.29 0.295508 0.000030
6 9 0.37 0.355536 0.000209
7 15 0.48 0.496828 0.000283
8 25 0.65 0.652385 0.000006
9 40 0.8 0.791843 0.000067
10 75 0.97 0.949751 0.000410
11 100 0.99 1.007135 0.000294
12 150 1.07 1.071898 0.000004 =SUM(D5..D12)
13
14 SSR 0.001303

FIGURA 20.4
Regresión no lineal para ajustar el modelo de la velocidad de crecimiento de saturación de
una levadura empleada en la producción comercial de cerveza.

el modelo y en los parámetros iniciales. Éstos se utilizan para generar una columna de
residuos al cuadrado que se suman, y el resultado se coloca en la celda D14. Después se
usa el Solver de Excel para minimizar la celda D14 al ajustar las celdas B1:B2. El resul-
= 1.23 y K = 22.14, con un
tado, como se muestra en la figura 20.4, da estimados de k máx
S = 0.001302. De esta forma, aunque, como se esperaba, la regresión no lineal ofrece
r
un ajuste ligeramente mejor, los resultados son casi idénticos. En otros casos, esto pue-

6/12/06 13:58:57
Chapra-20.indd 581
Chapra-20.indd 581 6/12/06 13:58:57