Page 769 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

25.3 MÉTODOS DE RUNGE-KUTTA 745

Observe que tal estimación de la pendiente es mucho más cercana al valor promedio en
el intervalo (4.4375), que la pendiente al inicio del intervalo (8.5) que se habría usado
con el procedimiento de Euler. La pendiente en el punto medio entonces se sustituye en
la ecuación (25.37) para predecir:

y(0.5) = 1 + 4.21875(0.5) = 3.109375 e = 3.4%
t
El cálculo se repite; los resultados se resumen en la figura 25.14 y en la tabla 25.3.
En el método de Ralston, k en el primer intervalo también es igual a 8.5 y [ecuación
1
(25.38b)]
2
3
k = –2(0.375) + 12(0.375) – 20(0.375) + 8.5 = 2.58203125
2
La pendiente promedio se calcula mediante:
1 2
φ = (. + ( 2 58203125. ) = 4 5546875.
85)
3 3
que se utiliza para predecir:

y(0.5) = 1 + 4.5546875(0.5) = 3.27734375 e = –1.82%
t
Los cálculos se repiten; los resultados se resumen en la figura 25.14 y en la tabla 25.3.
Observe que todos los métodos RK de segundo orden son superiores al método de Euler.

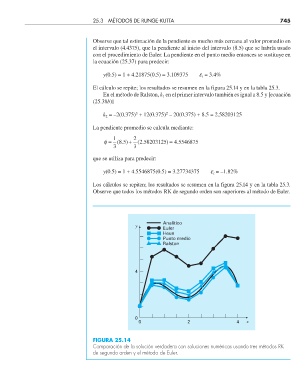
Analítico
y
Euler
Heun
Punto medio
Ralston

4

0
0 2 4 x

FIGURA 25.14
Comparación de la solución verdadera con soluciones numéricas usando tres métodos RK
de segundo orden y el método de Euler.

6/12/06 14:02:02
Chapra-25.indd 745
Chapra-25.indd 745 6/12/06 14:02:02