Page 935 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

31.2 APLICACIÓN DEL ELEMENTO FINITO EN UNA DIMENSIÓN 911

Solución. La ecuación a resolver es
2
dT =− 10
dx 2

Suponga una solución de la forma

T = ax + bx + c
2
la cual se deriva dos veces para obtener T″ = 2a. Sustituyendo este resultado en la ecua-
ción diferencial da a = –5. Las condiciones de frontera se utilizan para evaluar los co-
eficientes restantes. Para la primera condición en x = 0,

2
40 = –5(0) + b(0) + c
o c = 40. De manera similar, para la segunda condición,
200 = –5(10) + b(10) + 40
2
de donde se obtiene b = 66. Por lo tanto, la solución final es

2
T = –5x + 66x + 40
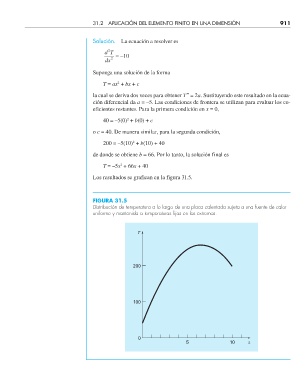
Los resultados se grafican en la figura 31.5.

FIGURA 31.5
Distribución de temperatura a lo largo de una placa calentada sujeta a una fuente de calor
uniforme y mantenida a temperaturas fi jas en los extremos.

T

200

100

0
5 10 x

6/12/06 14:05:15
Chapra-31.indd 911
Chapra-31.indd 911 6/12/06 14:05:15