Page 333 - APPLIED PROCESS DESIGN FOR CHEMICAL AND PETROCHEMICAL PLANTS, Volume 1, 3rd Edition

Mixing of Liquids 301

Table 5-1
Baffled Cylindrical Tanks
x, Ks
Viscous Turbulent
Propeller, 3.blade, pitch = diameter .... 41.0 0.32
Propeller, 3-blade, pitch = 2 diameters .. 43.5 1.00
Turbine, flat blade, 4 blades . 70.0 4.50
Turbine, flat blade, 6 blades . 71.0 6.30 0=4"
Turbine, flat blade, 8 blades . 72.0 7.80
Fan turbine, blades at 45\ 6 blades . 70.0 1.65
Shrouded turbine, stator ring . 172.5 1.12 0.025
-
Fl � )w1dle 4 2 � I ��� _( ���� l � - ��� -e}'. . 43.0 2.25 0.02
Flat paddles, 2 blades, D/W = 6 . 36.5 1.60
Flat paddles, 2 blades, D/W = 8 . 33.0 1.15
Flat paddles, 4 blades, D/W = 6 . 49.0 2.75 0.015
Flat paddles, 6 blades, D/W = 6 . 71.0 3.82

*By permission, R. H. Rushton and J. Y. Oldshue, Chem. Eng. 0.010 '.J=3"
Prag. 49, 161 (1953)
p

Oldshue [29] points out that to identify the turbulent
range as beginning at a specific NRe may not be exactly
correct, as it actually varies with different impeller 0.004
3
designs. This range may vary from N Re= 10 to N Re = 10 5,
so for common use 1\'Re = 10 is taken as the turbulent 0.003 P VS. N
5
range for all impellers. 0/T=l/3
C/0=1.0
Power Relationship �=1.0
U=l .O
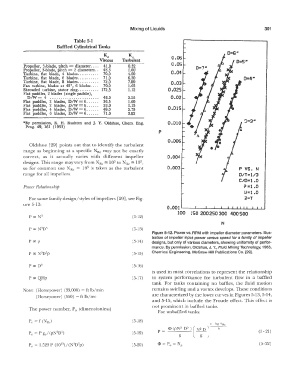
For same family design/styles of impellers [29], see Fig- i!=T
ure 5-12:
0.001'--�...__,_�L.-L.-.L....L....L..JL...LI-L...L.LI
100 1 so 200 250 300 400 500
P ex N 3 (5-12)
N
(5-13)
Figure 5-12. Power vs. RPM with impeller diameter parameters. Illus-
tration of impeller input power versus speed for a family of impeller
p (X p (5-14) designs, but only of various diameters, showing unifonnity of perfor-
mance. By permission, Oldshue, J. Y., Fluid Mixing Technology, 1983,
(5-15) Chemical Engineering, McGraw-Hill Publications Co. [29].
p (X 05 (5-16)
is used in most correlations to represent the relationship
P cx:QHp (5-17) to system performance for turbulent flow in a baffled
tank. For tanks containing no baffles, the fluid motion
Note: (Horsepower) (33,000) = ft lb/min remains swirling and a vortex develops. These conditions
(Horsepower) (550) = ft lb/sec are characterized by the lower curves in Figures 5-13, 3-14,
and 5-15, which include the Froude effect. This effect is
not prominent in baffled tanks.
The power number, P (dimensionless)
O
For unbaffled tanks:
(5-18)
a-log NRc
p = <l> (pNJ 05 ) ( N2 D) h
(5-19) (5- 21)
g g
(5-20) (5-22)