Page 11 - 2_studijní opora - modul 12

3.2.1 Tabulky četností

K základnímu uspořádání dat pomáhají tabulky četností. Ukážeme si příklad

tabulky vytvořené s pomocí čárkovací metody a dále příklad tabulky s intervaly.

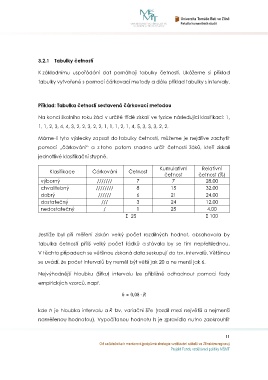
Příklad: Tabulka četností sestavená čárkovací metodou

Na konci školního roku žáci v určité třídě získali ve fyzice následující klasifikaci: 1,
1, 1, 2, 3, 4, 4, 3, 2, 2, 3, 2, 2, 1, 1, 1, 2, 1, 4, 5, 3, 3, 3, 2, 2.

Máme-li tyto výsledky zapsat do tabulky četností, můžeme je nejdříve zachytit

pomocí „čárkování“ a z toho potom snadno určit četnosti žáků, kteří získali
jednotlivé klasifikační stupně.

Kumulativní Relativní
Klasifikace Čárkování Četnost
četnost četnost (%)
výborný /////// 7 7 28,00
chvalitebný //////// 8 15 32,00
dobrý ////// 6 21 24,00
dostatečný /// 3 24 12,00
nedostatečný / 1 25 4,00
Σ 25 Σ 100

Jestliže byl při měření získán velký počet rozdílných hodnot, obsahovala by

tabulka četností příliš velký počet řádků a stávala by se tím nepřehlednou.
V těchto případech se většinou získaná data seskupují do tzv. intervalů. Většinou

se uvádí, že počet intervalů by neměl být větší jak 20 a ne menší jak 6.

Nejvýhodnější hloubku (šířku) intervalu lze přibližně odhadnout pomocí řady

empirických vzorců, např.

h  ,0 08  R

kde h je hloubka intervalu a R tzv. variační šíře (rozdíl mezi největší a nejmenší

naměřenou hodnotou). Vypočítanou hodnotu h je zpravidla nutno zaokrouhlit

11
Od začátečníka k mentorovi (podpůrné strategie vzdělávání učitelů ve Zlínském regionu)

Projekt Fondu vzdělávací politiky MŠMT