Page 163 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp
P. 163
Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
Ȁ
ǡ
Ǥ
ǡ ǡ ǯ
Ȁ Ǥ
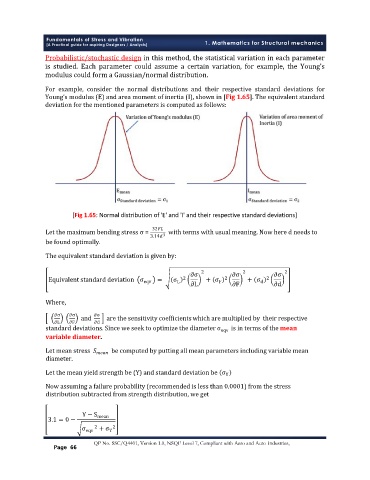
ǡ
ǯ ȋ Ȍ ȋ Ȍǡ ȏ ͳǤͷȐǤ
ǣ
[Fig 1.65: Normal distribution of 'E' and 'I' and their respective standard deviations]
Let the maximum bending stress s = 32 with terms with usual meaning. Now here d needs to
3.14 3
be found optimally.
The equivalent standard deviation is given by:
∂σ 2 ∂σ 2 ∂σ 2
2
2
2
Equivalent standard deviation σ eqv = σ + σ + σ
d
L
F
∂L ∂F ∂d
Where,
∂s ∂s ∂σ
and are the sensitivity coefficients which are multiplied by their respective
∂L ∂F ∂d
standard deviations. Since we seek to optimize the diameter σ eqv is in terms of the mean
variable diameter.
Let mean stress be computed by putting all mean parameters including variable mean
diameter.
Let the mean yield strength be (Y) and standard deviation be σ
Y
Now assuming a failure probability (recommended is less than 0.0001) from the stress
distribution subtracted from strength distribution, we get
Y − S
3.1 = 0 − mean
σ 2 + σ 2
eqv Y
QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 66