Page 167 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration
[A Practical guide for aspiring Designers / Analysts] 1. Mathematics for Structural mechanics
Substituting the values of the derivatives in the Hessian matrix, we get:

2
2
∂ f ∂ f
∂x 2 ∂x ∂y 2 0

2
Hessian Matrix = ∂ f ∂ f = 0 2
2
2
∂y ∂x ∂y

The determinant of the Hessian matrix is ‘4’ which is positive. Hence, at (x = 0) and (y = 0) the
function assumes a minimum value, and is given by:

f x, y = x + y + 2xy = 0
2
2
2

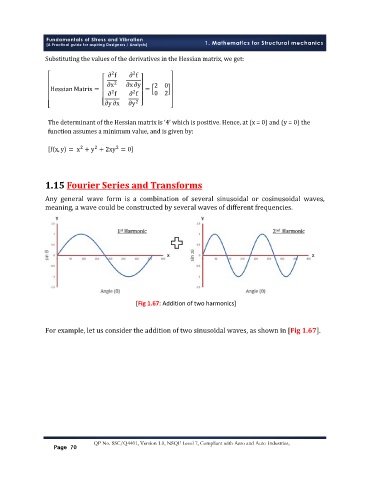
ͳǤͳͷ ‘—”‹‡” ‡”‹‡• ƒ† ”ƒ•ˆ‘”•

› ‰‡‡”ƒŽ ™ƒ˜‡ ˆ‘” ‹• ƒ ‘„‹ƒ–‹‘ ‘ˆ •‡˜‡”ƒŽ •‹—•‘‹†ƒŽ ‘” ‘•‹—•‘‹†ƒŽ ™ƒ˜‡•ǡ
‡ƒ‹‰ǡ ƒ ™ƒ˜‡ ‘—Ž† „‡ ‘•–”— –‡† „› •‡˜‡”ƒŽ ™ƒ˜‡• ‘ˆ †‹ˆˆ‡”‡– ˆ”‡“—‡ ‹‡•Ǥ

[Fig 1.67: Addition of two harmonics]

‘” ‡šƒ’Ž‡ǡ Ž‡– —• ‘•‹†‡” –Š‡ ƒ††‹–‹‘ ‘ˆ –™‘ •‹—•‘‹†ƒŽ ™ƒ˜‡•ǡ ƒ• •Š‘™ ‹ ȏ ‹‰ ͳǤ͸͹ȐǤ

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,
Page 70