Page 168 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Fundamentals of Stress and Vibration 1. Mathematics for Structural mechanics
[A Practical guide for aspiring Designers / Analysts]
Š‡ ‘„‹‡† ™ƒ˜‡ ˆ‘” ‘ˆ Šƒ”‘‹ • ͳ ƒ† ʹ ‹• ƒ• •Š‘™ ‹ ȏ ‹‰ ͳǤ͸ͺȐǤ

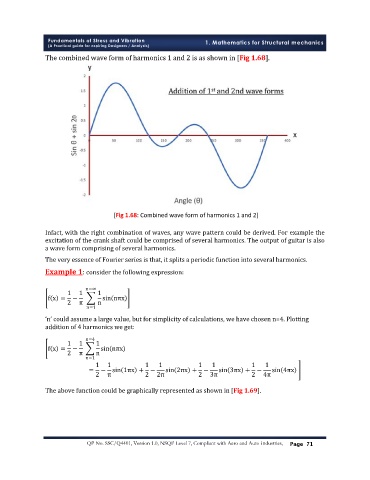
[Fig 1.68: Combined wave form of harmonics 1 and 2]

ˆƒ –ǡ ™‹–Š –Š‡ ”‹‰Š– ‘„‹ƒ–‹‘ ‘ˆ ™ƒ˜‡•ǡ ƒ› ™ƒ˜‡ ’ƒ––‡” ‘—Ž† „‡ †‡”‹˜‡†Ǥ ‘” ‡šƒ’Ž‡ –Š‡
‡š ‹–ƒ–‹‘ ‘ˆ –Š‡ ”ƒ •Šƒˆ– ‘—Ž† „‡ ‘’”‹•‡† ‘ˆ •‡˜‡”ƒŽ Šƒ”‘‹ •Ǥ Š‡ ‘—–’—– ‘ˆ ‰—‹–ƒ” ‹• ƒŽ•‘
ƒ ™ƒ˜‡ ˆ‘” ‘’”‹•‹‰ ‘ˆ •‡˜‡”ƒŽ Šƒ”‘‹ •Ǥ

Š‡ ˜‡”› ‡••‡ ‡ ‘ˆ ‘—”‹‡” •‡”‹‡• ‹• –Šƒ–ǡ ‹– •’Ž‹–• ƒ ’‡”‹‘†‹ ˆ— –‹‘ ‹–‘ •‡˜‡”ƒŽ Šƒ”‘‹ •Ǥ
šƒ’Ž‡ ͳǣ ‘•‹†‡” –Š‡ ˆ‘ŽŽ‘™‹‰ ‡š’”‡••‹‘ǣ

n=∞
1 1 1
f x = − sin nπx
2 π n
n=1
‘n’ could assume a large value, but for simplicity of calculations, we have chosen n=4. Plotting
addition of 4 harmonics we get:

n=4
1 1 1
f x = − sin nπx
2 π n
n=1
1 1 1 1 1 1 1 1
= − sin 1πx + − sin 2πx + − sin 3πx + − sin 4πx
2 π 2 2π 2 3π 2 4π

The above function could be graphically represented as shown in [Fig 1.69].

QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries, Page 71