Page 84 - C:\Users\trainee\AppData\Local\Temp\msoEAA3.tmp

Document Title
Fundamentals of Stress and Vibration Chapter Title
[A Practical guide for aspiring Designers / Analysts] 2. Engineering Mechanics

Š‡ ’‘–‡–‹ƒŽ Ž‘•– „› –Š‡ ›Ž‹†‡” ‹• ƒ• •Š‘™ ‹ ȏ ‹‰ ʹǤ͹ʹȐ

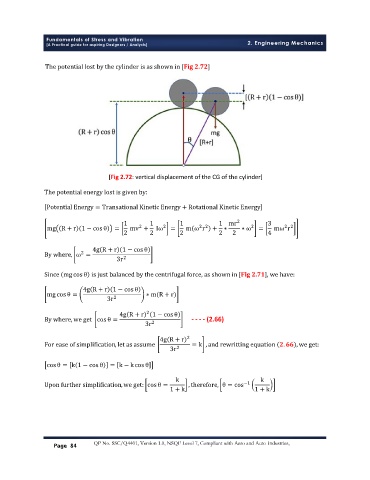
[Fig 2.72: vertical displacement of the CG of the cylinder]

The potential energy lost is given by:

Potential Energy = Transational Kinetic Energy + Rotational Kinetic Energy

1 1 1 1 mr 2 3
2
2
2 2
2
2 2
mg R + r 1 − cos θ = mv + Iω = m ω r + ∗ ∗ ω = mω r
2 2 2 2 2 4
4g R + r 1 − cos θ
2
By where, ω =
3r 2
Since mg cos θ is just balanced by the centrifugal force, as shown in [Fig 2.71], we have:
4g R + r 1 − cos θ
mg cos θ = ∗ m(R + r)
3r 2

2
4g R + r 1 − cos θ
By where, we get cos θ = - - - - (2.66)
3r 2
4g R + r 2
For ease of simplification, let as assume = k , and rewritting equation . , we get:
3r 2

cosθ = k 1 − cos θ = k − k cos θ

k k
Upon further simplification, we get: cosθ = , therefore, θ = cos −1
1 + k 1 + k

Page 84 QP No. SSC/Q4401, Version 1.0, NSQF Level 7, Compliant with Aero and Auto Industries,