Page 14 - Fisika Terapan for Engineers and Scientists

214 CHAPTER 7 Work and Energy

✔ Checkup 7.2
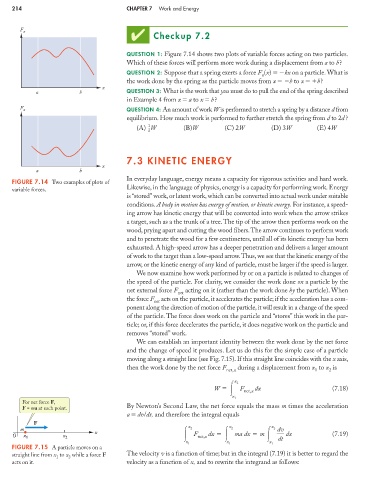
F x

QUESTION 1: Figure 7.14 shows two plots of variable forces acting on two particles.
Which of these forces will perform more work during a displacement from a to b?
QUESTION 2: Suppose that a spring exerts a force F (x) kx on a particle. What is
x
the work done by the spring as the particle moves from x b to x b?
x
a b QUESTION 3: What is the work that you must do to pull the end of the spring described
in Example 4 from x a to x b?
F x QUESTION 4: An amount of work W is performed to stretch a spring by a distance d from
equilibrium. How much work is performed to further stretch the spring from d to 2d ?
1
(A) W (B)W (C) 2W (D) 3W (E) 4W
2

7.3 KINETIC ENERGY
x
a b
In everyday language, energy means a capacity for vigorous activities and hard work.
FIGURE 7.14 Two examples of plots of
Likewise, in the language of physics, energy is a capacity for performing work. Energy
variable forces.
is “stored” work, or latent work, which can be converted into actual work under suitable
conditions. A body in motion has energy of motion, or kinetic energy. For instance, a speed-
ing arrow has kinetic energy that will be converted into work when the arrow strikes
a target, such as a the trunk of a tree.The tip of the arrow then performs work on the
wood, prying apart and cutting the wood fibers.The arrow continues to perform work
and to penetrate the wood for a few centimeters, until all of its kinetic energy has been
exhausted. A high-speed arrow has a deeper penetration and delivers a larger amount
of work to the target than a low-speed arrow.Thus, we see that the kinetic energy of the
arrow, or the kinetic energy of any kind of particle, must be larger if the speed is larger.
We now examine how work performed by or on a particle is related to changes of
the speed of the particle. For clarity, we consider the work done on a particle by the
net external force F acting on it (rather than the work done by the particle). When
net
the force F net acts on the particle, it accelerates the particle; if the acceleration has a com-
ponent along the direction of motion of the particle, it will result in a change of the speed
of the particle. The force does work on the particle and “stores” this work in the par-
ticle; or, if this force decelerates the particle, it does negative work on the particle and
removes “stored” work.
We can establish an important identity between the work done by the net force
and the change of speed it produces. Let us do this for the simple case of a particle
moving along a straight line (see Fig. 7.15). If this straight line coincides with the x axis,
then the work done by the net force F net,x during a displacement from x to x is
2
1
x 2
W F net,x dx (7.18)
x 1
For net force F,
F = ma at each point. By Newton’s Second Law, the net force equals the mass m times the acceleration
a dv/dt, and therefore the integral equals
F
m x 2 x 2 x 2 dv
x dx
O x 1 x 2 F net,x ma dx m dt dx (7.19)
x 1 x 1 x 1
FIGURE 7.15 A particle moves on a
straight line from x to x while a force F The velocity v is a function of time; but in the integral (7.19) it is better to regard the
1 2
acts on it. velocity as a function of x, and to rewrite the integrand as follows: