Page 211 - Fisika Terapan for Engineers and Scientists

13.4 Torque and Angular Momentum as Vectors 411

According to the definition of the cross product, the magnitude of is

t rF sin u (13.36)

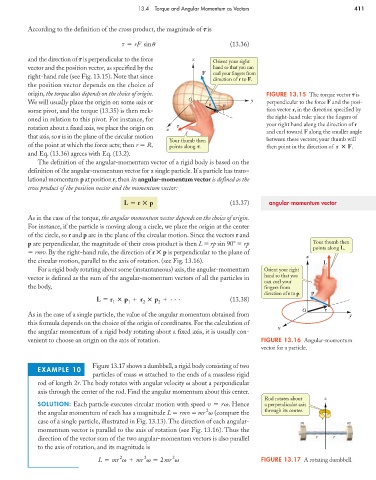
and the direction of is perpendicular to the force z Orient your right
vector and the position vector, as specified by the hand so that you can
F curl your fingers from
right-hand rule (see Fig. 13.15). Note that since
direction of r to F.
the position vector depends on the choice of
origin, the torque also depends on the choice of origin. FIGURE 13.15 The torque vector is
We will usually place the origin on some axis or O y perpendicular to the force F and the posi-
r u
some pivot, and the torque (13.35) is then reck- tion vector r, in the direction specified by
oned in relation to this pivot. For instance, for the right-hand rule: place the fingers of
rotation about a fixed axis, we place the origin on x t your right hand along the direction of r
and curl toward F along the smaller angle
that axis, so r is in the plane of the circular motion
Your thumb then between these vectors; your thumb will
of the point at which the force acts; then r R, points along t. then point in the direction of r F.
and Eq. (13.36) agrees with Eq. (13.2).
The definition of the angular-momentum vector of a rigid body is based on the
definition of the angular-momentum vector for a single particle. If a particle has trans-
lational momentum p at position r, then its angular-momentum vector is defined as the
cross product of the position vector and the momentum vector:
L r p (13.37) angular-momentum vector

As in the case of the torque, the angular momentum vector depends on the choice of origin.
For instance, if the particle is moving along a circle, we place the origin at the center
of the circle, so r and p are in the plane of the circular motion. Since the vectors r and
p are perpendicular, the magnitude of their cross product is then L rp sin 90 rp Your thumb then
points along L.
rmv. By the right-hand rule, the direction of r p is perpendicular to the plane of
z
the circular motion, parallel to the axis of rotation. (see Fig. 13.16). L
For a rigid body rotating about some (instantaneous) axis, the angular-momentum Orient your right
vector is defined as the sum of the angular-momentum vectors of all the particles in hand so that you
can curl your
the body, fingers from
direction of r to p. p
L r p r p # # # (13.38)
1 1 2 2
O r
As in the case of a single particle, the value of the angular momentum obtained from y
this formula depends on the choice of the origin of coordinates. For the calculation of
x
the angular momentum of a rigid body rotating about a fixed axis, it is usually con-
venient to choose an origin on the axis of rotation. FIGURE 13.16 Angular-momentum
vector for a particle.

Figure 13.17 shows a dumbbell, a rigid body consisting of two
EXAMPLE 10
particles of mass m attached to the ends of a massless rigid
rod of length 2r. The body rotates with angular velocity about a perpendicular
axis through the center of the rod. Find the angular momentum about this center.
Rod rotates about z
SOLUTION: Each particle executes circular motion with speed v r . Hence a perpendicular axis
2
the angular momentum of each has a magnitude L rmv mr (compare the through its center.
case of a single particle, illustrated in Fig. 13.13). The direction of each angular- m m
momentum vector is parallel to the axis of rotation (see Fig. 13.16). Thus the
direction of the vector sum of the two angular-momentum vectors is also parallel r r
to the axis of rotation, and its magnitude is
2
2
2
L mr mr 2mr FIGURE 13.17 A rotating dumbbell.