Page 236 - Fisika Terapan for Engineers and Scientists

436 CHAPTER 14 Statics and Elasticity

that the counterweights are placed on the short arm as in the preceding example:
(a)
the fixed counterweight of 100 metric tons is at the end of the arm, and the mobile
counterweight of 120 metric tons is at a distance of 21 m from the centerline.
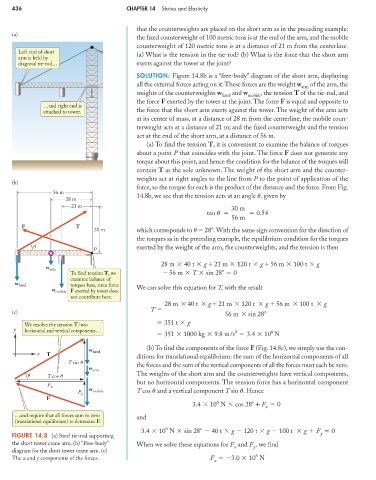
Left end of short
arm is held by (a) What is the tension in the tie-rod? (b) What is the force that the short arm
diagonal tie-rod… exerts against the tower at the joint?
SOLUTION: Figure 14.8b is a “free-body” diagram of the short arm, displaying
all the external forces acting on it.These forces are the weight w of the arm, the
arm
weights of the counterweights w and w , the tension T of the tie-rod, and
fixed mobile
the force F exerted by the tower at the joint. The force F is equal and opposite to
…and right end is
attached to tower. the force that the short arm exerts against the tower. The weight of the arm acts
at its center of mass, at a distance of 28 m from the centerline; the mobile coun-
terweight acts at a distance of 21 m; and the fixed counterweight and the tension
act at the end of the short arm, at a distance of 56 m.
(a) To find the tension T, it is convenient to examine the balance of torques
about a point P that coincides with the joint. The force F does not generate any
torque about this point, and hence the condition for the balance of the torques will
contain T as the sole unknown. The weight of the short arm and the counter-
weights act at right angles to the line from P to the point of application of the
(b)
force, so the torque for each is the product of the distance and the force. From Fig.
56 m
14.8b, we see that the tension acts at an angle , given by
28 m
21 m 30 m
tan u 0.54
56 m
F T
30 m which corresponds to 28 . With the same sign convention for the direction of
the torques as in the preceding example, the equilibrium condition for the torques
u exerted by the weight of the arm, the counterweights, and the tension is then
P
28 m 40 t g 21 m 120 t g 56 m 100 t g
w arm
To find tension T, we 56 m T sin 28 0
examine balance of
w fixed torques here, since force
w mobile F exerted by tower does We can solve this equation for T, with the result
not contribute here.
28 m 40 t g 21 m 120 t g 56 m 100 t g
T
(c) 56 m sin 2 8
We resolve the tension T into 351 t g
y horizontal and vertical components… 2 6
351 1000 kg 9.8 m /s 3.4 10 N
w (b) To find the components of the force F (Fig. 14.8c), we simply use the con-
x T fixed
ditions for translational equilibrium: the sum of the horizontal components of all
T sin u
w arm the forces and the sum of the vertical components of all the forces must each be zero.
u T cos u The weights of the short arm and the counterweights have vertical components,
but no horizontal components. The tension force has a horizontal component
F x
F y w mobile T cos and a vertical component T sin . Hence
F
6
3.4 10 N cos 28 F 0
x
…and require that all forces sum to zero and
(translational equilibrium) to determine F.
6
3.4 10 N sin 28 40 t g 120 t g 100 t g F 0
FIGURE 14.8 (a) Steel tie-rod supporting y
the short tower crane arm. (b) “Free-body” When we solve these equations for F and F , we find
y
x
diagram for the short tower crane arm. (c)
6
The x and y components of the forces. F 3.0 10 N
x