Page 89 - Fisika Terapan for Engineers and Scientists

9.5 Energy in Orbital Motion 289

We already have evaluated this kind of integral in Example 2 of Chapter 8 (in the case
of the gravitational force, the constant A in that example is A GMm). The result
of the integration is
GMm r 2 GMm GMm
W ` (9.19)
x r r
r 1 2 1
As expected, this result shows that the work is the difference between two potential ener-
gies. Accordingly, we can identify the gravitational potential energy as

GMm
(9.20) gravitational potential energy
U
r
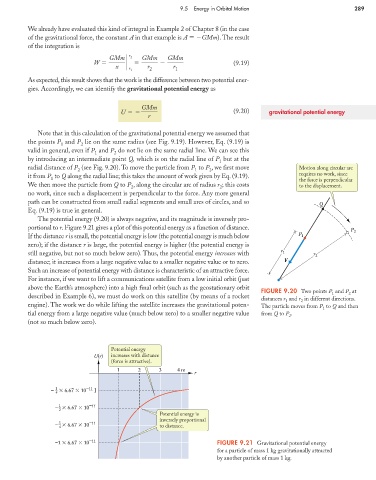
Note that in this calculation of the gravitational potential energy we assumed that
the points P and P lie on the same radius (see Fig. 9.19). However, Eq. (9.19) is
1 2
valid in general, even if P and P do not lie on the same radial line. We can see this
1 2
by introducing an intermediate point Q, which is on the radial line of P but at the
1
radial distance of P (see Fig. 9.20).To move the particle from P to P , we first move Motion along circular arc
2 1 2
it from P to Q along the radial line; this takes the amount of work given by Eq. (9.19). requires no work, since
1 the force is perpendicular
We then move the particle from Q to P , along the circular arc of radius r ; this costs to the displacement.
2 2
no work, since such a displacement is perpendicular to the force. Any more general
path can be constructed from small radial segments and small arcs of circles, and so Q
Eq. (9.19) is true in general.
The potential energy (9.20) is always negative, and its magnitude is inversely pro-
portional to r. Figure 9.21 gives a plot of this potential energy as a function of distance.
P 2
If the distance r is small, the potential energy is low (the potential energy is much below P 1
zero); if the distance r is large, the potential energy is higher (the potential energy is
still negative, but not so much below zero). Thus, the potential energy increases with r 1 r 2
distance; it increases from a large negative value to a smaller negative value or to zero. F
Such an increase of potential energy with distance is characteristic of an attractive force.
For instance, if we want to lift a communications satellite from a low initial orbit (just
above the Earth’s atmosphere) into a high final orbit (such as the geostationary orbit
FIGURE 9.20 Two points P and P at
1
2
described in Example 6), we must do work on this satellite (by means of a rocket
distances r and r in different directions.
2
1
engine). The work we do while lifting the satellite increases the gravitational poten- The particle moves from P to Q and then
1
tial energy from a large negative value (much below zero) to a smaller negative value from Q to P .
2
(not so much below zero).
Potential energy
U(r) increases with distance
(force is attractive).
1 2 3 4 m
r

1
– 6.67 10 –11
4
1
– 6.67 10 –11
2
Potential energy is
inversely proportional
3
– 6.67 10 –11 to distance.
4
–1 6.67 10 –11 FIGURE 9.21 Gravitational potential energy
for a particle of mass 1 kg gravitationally attracted
by another particle of mass 1 kg.