Page 87 - Fisika Terapan for Engineers and Scientists

9.4 Elliptical Orbits; Kepler’s Laws 287

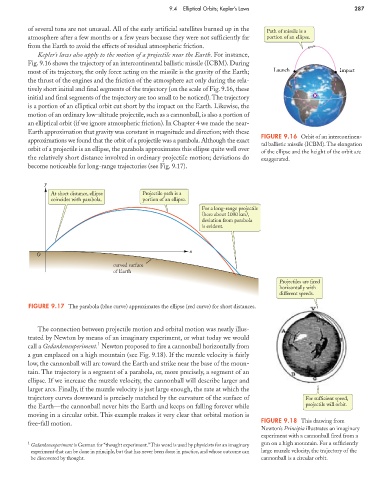
of several tons are not unusual. All of the early artificial satellites burned up in the Path of missile is a
atmosphere after a few months or a few years because they were not sufficiently far portion of an ellipse.
from the Earth to avoid the effects of residual atmospheric friction.
Kepler’s laws also apply to the motion of a projectile near the Earth. For instance,
Fig. 9.16 shows the trajectory of an intercontinental ballistic missile (ICBM). During
most of its trajectory, the only force acting on the missile is the gravity of the Earth; Launch Impact
the thrust of the engines and the friction of the atmosphere act only during the rela-
tively short initial and final segments of the trajectory (on the scale of Fig. 9.16, these
initial and final segments of the trajectory are too small to be noticed).The trajectory
is a portion of an elliptical orbit cut short by the impact on the Earth. Likewise, the
motion of an ordinary low-altitude projectile, such as a cannonball, is also a portion of
an elliptical orbit (if we ignore atmospheric friction). In Chapter 4 we made the near-
Earth approximation that gravity was constant in magnitude and direction; with these
FIGURE 9.16 Orbit of an intercontinen-
approximations we found that the orbit of a projectile was a parabola. Although the exact
tal ballistic missile (ICBM). The elongation
orbit of a projectile is an ellipse, the parabola approximates this ellipse quite well over
of the ellipse and the height of the orbit are
the relatively short distance involved in ordinary projectile motion; deviations do exaggerated.
become noticeable for long-range trajectories (see Fig. 9.17).

y
At short distance, ellipse Projectile path is a
coincides with parabola. portion of an ellipse.
For a long-range projectile
(here about 1000 km),
deviation from parabola
is evident.

x
O
curved surface
of Earth
Projectiles are fired
horizontally with
different speeds.
FIGURE 9.17 The parabola (blue curve) approximates the ellipse (red curve) for short distances.

The connection between projectile motion and orbital motion was neatly illus-
trated by Newton by means of an imaginary experiment, or what today we would
1
call a Gedankenexperiment. Newton proposed to fire a cannonball horizontally from
a gun emplaced on a high mountain (see Fig. 9.18). If the muzzle velocity is fairly
low, the cannonball will arc toward the Earth and strike near the base of the moun-
tain. The trajectory is a segment of a parabola, or, more precisely, a segment of an
ellipse. If we increase the muzzle velocity, the cannonball will describe larger and
larger arcs. Finally, if the muzzle velocity is just large enough, the rate at which the
trajectory curves downward is precisely matched by the curvature of the surface of For sufficient speed,
the Earth—the cannonball never hits the Earth and keeps on falling forever while projectile will orbit.
moving in a circular orbit. This example makes it very clear that orbital motion is
free-fall motion. FIGURE 9.18 This drawing from
Newton’s Principia illustrates an imaginary
experiment with a cannonball fired from a
1 gun on a high mountain. For a sufficiently
Gedankenexperiment is German for “thought experiment.”This word is used by physicists for an imaginary
experiment that can be done in principle, but that has never been done in practice, and whose outcome can large muzzle velocity, the trajectory of the
be discovered by thought. cannonball is a circular orbit.