Page 43 - Fisica_1_BGU

3.3. Movimiento circular uniforme

En nuestra vida cotidiana existen muchos movimientos en los que un móvil se desplaza siguiendo una
trayectoria con forma de circunferencia. Por ejemplo, una rueda, un tiovivo, una noria, las cuchillas de una
batidora. Este movimiento recibe el nombre de movimiento circular.

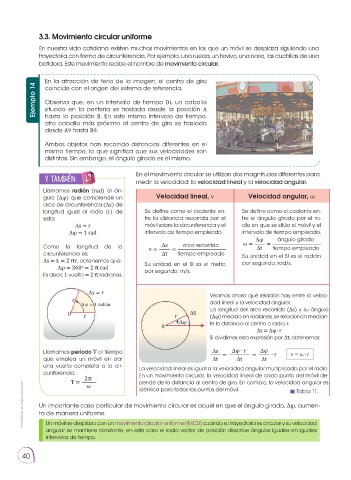
En la atracción de feria de la imagen, el centro de giro
Ejemplo 14 Observa que, en un intervalo de tiempo Dt, un caballo
coincide con el origen del sistema de referencia.

situado en la periferia se traslada desde la posición A
hasta la posición B. En este mismo intervalo de tiempo,
otro caballo más próximo al centro de giro se traslada
desde A9 hasta B9. O
A' ∆s'
Ambos objetos han recorrido distancias diferentes en el A B'
mismo tiempo, lo que significa que sus velocidades son ∆s B
distintas. Sin embargo, el ángulo girado es el mismo.

CALCULADORA
EN GRUPO Y TAMBIÉN TICS RECORTABLES En el movimiento circular se utilizan dos magnitudes diferentes para
y también: medir la velocidad: la velocidad lineal y la velocidad angular.
Llamamos radián (rad) al án-
gulo (∆φ) que comprende un Velocidad lineal, v Velocidad angular, ω
arco de circunferencia (∆s) de
longitud igual al radio (r) de Se define como el cociente en- Se define como el cociente en-
esta: tre la distancia recorrida por el tre el ángulo girado por el ra-
∆s = r móvil sobre la circunferencia y el dio en que se sitúa el móvil y el
∆φ = 1 rad intervalo de tiempo empleado. intervalo de tiempo empleado.
∆φ ángulo girado
Como la longitud de la v = ∆s = arco recorrido ω = ∆t = tiempo empleado
circunfe rencia es: ∆t tiempo empleado Su unidad en el SI es el radián
∆s = L = 2 �r, obtenemos que: Su unidad en el SI es el metro por segundo, rad/s.
o
∆φ = 360 = 2 � rad por segundo, m/s.
Es decir, 1 vuelta = 2 � radianes.

∆s = r
Veamos ahora qué relación hay entre la veloci-
r dad lineal y la velocidad angular.
∆ φ = 1 radián
∆s La longitud del arco recorrido (∆s) y su ángulo
0 (∆φ) medido en radianes, se relacionan median-
r r
∆φ te la distancia al centro o radio, r.
0
∆s = ∆φ ∙ r
Si dividimos esta expresión por ∆t, obtenemos:

Llamamos período T al tiempo ∆s = ∆φ ∙ r = ∆φ ∙ r v = ω ∙ r
que emplea un móvil en dar ∆t ∆t ∆t
una vuelta completa a la cir- La velocidad lineal es igual a la velocidad angular multiplicada por el radio.
cunferencia. En un movimiento circular, la velocidad lineal de cada punto del móvil de-
2� pende de la distancia al centro de giro. En cambio, la velocidad angular es
Prohibida su reproducción Un importante caso particular de movimiento circular es aquel en que el ángulo girado, ∆φ, aumen-
T =
ω
idéntica para todos los puntos del móvil.
Tabla 11.
ta de manera uniforme.
Un móvil se desplaza con un movimiento circular uniforme (MCU) cuando su trayectoria es circular y su velocidad
angular se mantiene constante, en este caso el radio vector de posición describe ángulos iguales en iguales
intervalos de tiempo.

40