Page 41 - Fisica_1_BGU

EN GRUPO Y TAMBIÉN TICS RECORTABLES CALCULADORA
y también: El movimiento vertical de los cuerpos

Si dejamos caer un cuerpo este describe, por la acción de la gra-
Galileo ideó experimentos
con planos inclinados que vedad, un movimiento rectilíneo uniformemente acelerado, lla-
le permitían estudiar más fá- mado caída libre, cuya aceleración constante es la aceleración
cilmente la caída libre de los de la gravedad, g = 9,8 m/s .
2
cuerpos. Comprobó que la
velocidad final que adquie- Lo mismo sucede si el cuerpo se lanza verticalmente hacia arriba
re un cuerpo al bajar por un o hacia abajo.
plano inclinado es la misma En el estudio de esta clase de movimientos se acostumbra a to-
que si se deja caer libremen-
te en vertical desde la misma mar un sistema de referencia con origen en el suelo y formado
altura que el plano inclinado. por un eje de coordenadas, cuyo sentido positivo es el que se
En ambos casos, el móvil de- dirige hacia arriba.
sarrolla un MRUA, aunque la
aceleración es distinta: en el Las ecuaciones de este movimiento para el sistema de referencia
caso del plano, depende de mencionado son las del MRUA para una aceleración negativa,
2
su inclinación; mientras que a = -g = -9,8 m/s .
en caída libre, la aceleración
1
vale g. v = v - g ∙ t x = x + v ∙t - g ∙ t 2
0 0 0
2
Según el sentido de la velocidad inicial, podemos tener tres casos:

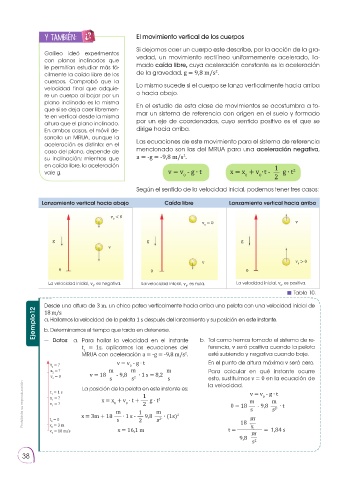
Lanzamiento vertical hacia abajo Caída libre Lanzamiento vertical hacia arriba

v < 0
0
v = 0 v
0
g g g
v

v v > 0
0
0 0 0
La velocidad inicial, v , es negativa. La velocidad inicial, v , es nula. La velocidad inicial, v , es positiva.
0 0 0
Tabla 10.

Desde una altura de 3 m, un chico patea verticalmente hacia arriba una pelota con una velocidad inicial de
Ejemplo12 a. Hallamos la velocidad de la pelota 1 s después del lanzamiento y su posición en este instante.
18 m/s.

b. Determinamos el tiempo que tarda en detenerse.
— Datos: a. Para hallar la velocidad en el instante
ferencia, v será positiva cuando la pelota
t = 1s, aplicamos las ecuaciones del b. Tal como hemos tomado el sistema de re-
1
MRUA con aceleración a = -g = -9,8 m/s . esté subiendo y negativa cuando baje.
2
v = v - g ∙ t En el punto de altura máxima v será cero.
t = ?
2 0
x = ? m m m Para calcular en qué instante ocurre
2
v = 18 - 9,8 ∙ 1 s = 8,2
v = 0 esto, sustituimos v = 0 en la ecuación de
2
s
s
s
2 La posición de la pelota en este instante es: la velocidad.
Prohibida su reproducción t = 1 s x = 3m + 18 ∙ 1 s - 9,8 ∙ (1s) 2 0 = 18 - 9,8 ∙ t
v = v - g ∙ t
1
1
0
x = ?
2
x = x + v ∙ t + g ∙ t
1
m
m
0
0
v = ?
2
1
2
s
s
m
m
1
t = 0
2
0
x = 3 m
s
0
v = 18 m/s s x = 16,1 m s 2 t = 18 m = 1,84 s
0
m
9,8
s 2
38