Page 45 - Fisica_1_BGU

Problemas resueltos

A

Dos automóviles salen al mismo tiempo de dos ciuda- a. Los dos vehículos se encuentran cuando sus posi-
des, A y B, separadas por una distancia de 192 km. ciones coinciden, es decir:
El primer automóvil sale de A hacia B a 75 km/h. El x = x = x ; 75 t = 192 - 85 t
segundo sale de B hacia A a 85 km/h. 1 2 192
a. Calcula en qué punto y en qué instante se 75 t + 85 t = 192 ; 160 t = 192 ; t = = 1,2 h
encuentran. 160
b. Representa en una gráfica posición-tiempo el mo- Los dos vehículos se encuentran 1,2 h después de su
vimiento de los dos vehículos. salida.
Solución
Para saber qué posición ocupan en este instante, sus-
— Datos : tituimos el valor de t en una ecuación cualquiera del
movimiento. Por ejemplo:
A P B km
x = 75 ∙ t = 75 ∙ 1,2 h = 90 km
x
= 0 x = ? h
01
t = 0 t = ?
Los dos vehículos se encuentran a 90 km de la ciudad A.
01
A P B
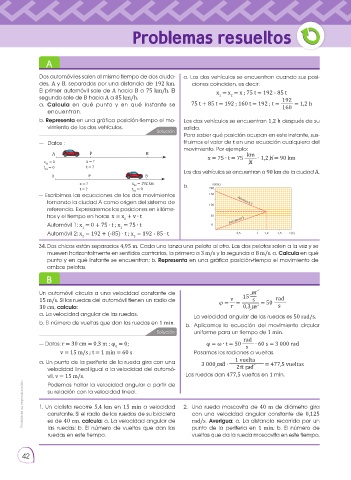
x = ? x = 192 km b. x(Km)
02
t = ? t = 0 200
02
— Escribimos las ecuaciones de los dos movimientos 150
tomando la ciudad A como origen del sistema de Automovil 2
100
referencia. Expresaremos las posiciones en kilóme-
tros y el tiempo en horas. x = x + v ∙ t 50
0 Automovil 1
Automóvil 1: x = 0 + 75 ∙ t ; x = 75 ∙ t 0
1 1
Automóvil 2: x = 192 + (-85) ∙ t ; x = 192 - 85 ∙ t 0,5 1 1,2 1,5 t(h)
2 2
34. Dos chicos están separados 4,95 m. Cada uno lanza una pelota al otro. Las dos pelotas salen a la vez y se
mueven horizontalmente en sentidos contrarios, la primera a 3 m/s y la segunda a 8 m/s. a. Calcula en qué
punto y en qué instante se encuentran; b. Representa en una gráfica posición-tiempo el movimiento de
ambas pelotas.
B
Un automóvil circula a una velocidad constante de m
15 m/s. Si las ruedas del automóvil tienen un radio de φ = v = 15 s = 50 rad
30 cm, calcula: r 0,3 m s
a. La velocidad angular de las ruedas. La velocidad angular de las ruedas es 50 rad/s.
b. El número de vueltas que dan las ruedas en 1 min. b. Aplicamos la ecuación del movimiento circular
Solución uniforme para un tiempo de 1 min.
rad
— Datos: r = 30 cm = 0,3 m ; φ = 0; φ = ω ∙ t = 50 ∙ 60 s = 3 000 rad
0 s
v = 15 m/s ; t = 1 min = 60 s Pasamos los radianes a vueltas.
a. Un punto de la periferia de la rueda gira con una 3 000 rad ∙ 1 vuelta = 477,5 vueltas
velocidad lineal igual a la velocidad del automó- 2� rad
vil, v = 15 m/s. Las ruedas dan 477,5 vueltas en 1 min.
Prohibida su reproducción 1. Un ciclista recorre 5,4 km en 15 min a velocidad 2. Una rueda moscovita de 40 m de diámetro gira
Podemos hallar la velocidad angular a partir de

su relación con la velocidad lineal.

constante. Si el radio de las ruedas de su bicicleta
con una velocidad angular constante de 0,125
es de 40 cm, calcula: a. La velocidad angular de
punto de la periferia en 1 min; b. El número de
las ruedas; b. El número de vueltas que dan las
ruedas en este tiempo. rad/s. Averigua: a. La distancia recorrida por un
vueltas que da la rueda moscovita en este tiempo.

42