Page 7 - FOCUS KSSM TG 4 MATEMATIK TAMBAHAN

Matematik Tambahan Tingkatan 4 Bab 7 Geometri Koordinat

Tip SPM 3 + x = 3 dan –24 + y = –5
4 4
Diberi P ialah titik yang membahagikan garis x = 9 y = 4
tembereng AB,
• jika mAP = nPB, maka AP : PB = n : m Maka, C = (9, 4)

m Cuba Soalan 7 dalam ‘Cuba ini! 7.1’
n B
m

A n P PB = — AB C Menyelesaikan masalah melibatkan
n
AP = — PB
m pembahagi tembereng garis
Kuasai SPM 2015
• jika mAB = nAP, maka AP : PB = m : n – m Kertas 1 SPM
n m Rajah menunjukkan kedudukan dua orang penunggang
m B basikal, A dan B.
A P y
n
A(–6, 7)
Cuba Soalan 5 – 6 dalam ‘Cuba ini! 7.1’
x
0
5 B(9, –3)
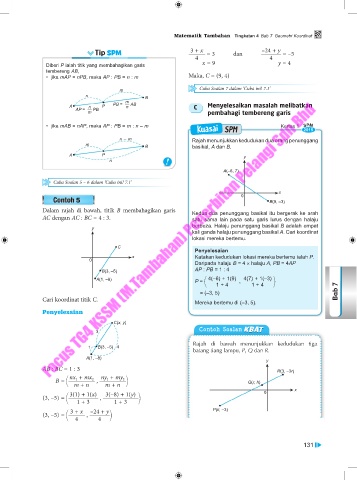
Dalam rajah di bawah, titik B membahagikan garis Kedua-dua penunggang basikal itu bergerak ke arah
AC dengan AC : BC = 4 : 3. satu sama lain pada satu garis lurus dengan halaju

y berbeza. Halaju penunggang basikal B adalah empat
kali ganda halaju penunggang basikal A. Cari koordinat
lokasi mereka bertemu.
C
Penyelesaian
x Katakan kedudukan lokasi mereka bertemu ialah P.
0
Daripada halaju B = 4 × halaju A, PB = 4AP
B(3, –5) AP : PB = 1 : 4
A(1, –8) P = 1 4(–6) + 1(9) , 4(7) + 1(–3) 2
1 + 4
1 + 4
= (–3, 5) Bab 7
Cari koordinat titik C.
Mereka bertemu di (–3, 5).
Penyelesaian

C(x, y)
Contoh Soalan KBAT
KBAT
3
Rajah di bawah menunjukkan kedudukan tiga
1 B(3, –5) 4
batang tiang lampu, P, Q dan R.
A(1, –8)
y
AB : BC = 1 : 3 R(3, –3r)

B = 1 nx 1 + mx 2 , ny 1 + my 2 2 Q(r, h)
m + n
m + n
x
0
(3, –5) = 1 3(1) + 1(x) , 3(–8) + 1(y) 2
1 + 3
1 + 3
(3, –5) = 1 3 + x , –24 + y 2 P(k, –3)
4
4
131