Page 146 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

122 MÉTODOS CERRADOS

Las técnicas gráficas tienen un valor práctico limitado, ya que no son precisas. Sin
f (x)
embargo, los métodos gráficos se utilizan para obtener aproximaciones de la raíz. Dichas
aproximaciones se pueden usar como valores iniciales en los métodos numéricos anali-
zados en este capítulo y en el siguiente.
Las interpretaciones gráficas, además de proporcionar estimaciones de la raíz, son
herramientas importantes en la comprensión de las propiedades de las funciones y en la
x
a) prevención de las fallas de los métodos numéricos. Por ejemplo, la figura 5.2 muestra
algunas de las formas en las que la raíz puede encontrarse (o no encontrarse) en un in-
f (x)
u
tervalo definido por un límite inferior x l y un límite superior x . La figura 5.2b repre-
senta el caso en que una sola raíz está acotada por los valores positivo y negativo de f(x).
) y f(x ) están también en lados opuestos del eje
Sin embargo, la figura 5.2d, donde f(x l u
x, muestra tres raíces que se presentan en ese intervalo. En general, si f(x ) y f(x ) tienen
l
u
x signos opuestos, existe un número impar de raíces en el intervalo. Como se indica en las
b) figuras 5.2a y c, si f(x ) y f(x ) tienen el mismo signo, no hay raíces o hay un número par
l
u
de ellas entre los valores.
f (x)
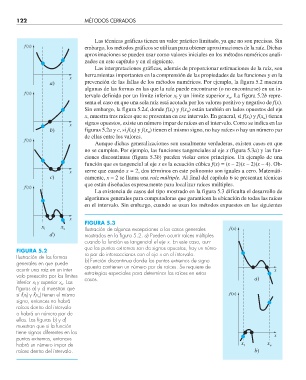
Aunque dichas generalizaciones son usualmente verdaderas, existen casos en que
no se cumplen. Por ejemplo, las funciones tangenciales al eje x (figura 5.3a) y las fun-
ciones discontinuas (figura 5.3b) pueden violar estos principios. Un ejemplo de una
función que es tangencial al eje x es la ecuación cúbica f(x) = (x – 2)(x – 2)(x – 4). Ob-
x serve que cuando x = 2, dos términos en este polinomio son iguales a cero. Matemáti-
c) camente, x = 2 se llama una raíz múltiple. Al final del capítulo 6 se presentan técnicas
que están diseñadas expresamente para localizar raíces múltiples.
f (x)
La existencia de casos del tipo mostrado en la figura 5.3 dificulta el desarrollo de
algoritmos generales para computadoras que garanticen la ubicación de todas las raíces
en el intervalo. Sin embargo, cuando se usan los métodos expuestos en las siguientes
x
FIGURA 5.3
x x
l u Ilustración de algunas excepciones a los casos generales f (x)
d) mostrados en la fi gura 5.2. a) Pueden ocurrir raíces múltiples
cuando la función es tangencial el eje x. En este caso, aun-
que los puntos extremos son de signos opuestos, hay un núme-
FIGURA 5.2
Ilustración de las formas ro par de intersecciones con el eje x en el intervalo.
generales en que puede b) Función discontinua donde los puntos extremos de signo
ocurrir una raíz en un inter- opuesto contienen un número par de raíces. Se requiere de x
valo preescrito por los límites estrategias especiales para determinar las raíces en estos a)
inferior x l y superior x u . Las casos.
fi guras a) y c) muestran que
si f(x l ) y f(x u ) tienen el mismo f (x)
signo, entonces no habrá
raíces dentro del intervalo
o habrá un número par de
ellas. Las fi guras b) y d)
muestran que si la función
tiene signos diferentes en los x
puntos extremos, entonces
habrá un número impar de x l x u
raíces dentro del intervalo. b)

6/12/06 13:49:19
Chapra-05.indd 122 6/12/06 13:49:19
Chapra-05.indd 122