Page 145 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

5.1 MÉTODOS GRÁFICOS 121

c f(c)
4 34.115
8 17.653
12 6.067
16 –2.269
20 –8.401

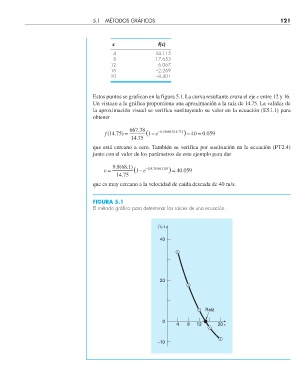
Estos puntos se grafican en la figura 5.1. La curva resultante cruza el eje c entre 12 y 16.
Un vistazo a la gráfica proporciona una aproximación a la raíz de 14.75. La validez de
la aproximación visual se verifica sustituyendo su valor en la ecuación (E5.1.1) para
obtener

f (. )14 75 = 667 .38 (1 – e –.0 146843 ( .14 75 ) – ) 40 = . 0 059
14 .75
que está cercano a cero. También se verifica por sustitución en la ecuación (PT2.4)
junto con el valor de los parámetros de este ejemplo para dar

.(
v = 9 8 68 1 . ) ( 1– e –( 14 75 68 1 10. / . ) ) = 40 059
.
14 75
.
que es muy cercano a la velocidad de caída deseada de 40 m/s.
FIGURA 5.1
El método gráfi co para determinar las raíces de una ecuación.

f(c)

40

20

Raíz

0
4 8 12 20 c

–10

6/12/06 13:49:19
Chapra-05.indd 121
Chapra-05.indd 121 6/12/06 13:49:19