Page 166 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

CAPÍTULO 6

Métodos abiertos

En los métodos cerrados del capítulo anterior la raíz se encuentra dentro de un interva-
lo predeterminado por un límite inferior y otro superior. La aplicación repetida de estos
métodos siempre genera aproximaciones cada vez más cercanas a la raíz. Se dice que
tales métodos son convergentes porque se acercan progresivamente a la raíz a medida
que se avanza en el cálculo (figura 6.1a).
En contraste, los métodos abiertos descritos en este capítulo se basan en fórmulas
que requieren únicamente de un solo valor de inicio x o que empiecen con un par de
ellos, pero que no necesariamente encierran la raíz. Éstos, algunas veces divergen o se
alejan de la raíz verdadera a medida que se avanza en el cálculo (figura 6.1b). Sin em-
bargo, cuando los métodos abiertos convergen (figura 6.1c), en general lo hacen mucho
más rápido que los métodos cerrados. Empecemos el análisis de los métodos abiertos
con una versión simple que es útil para ilustrar su forma general y también para demos-
trar el concepto de convergencia.

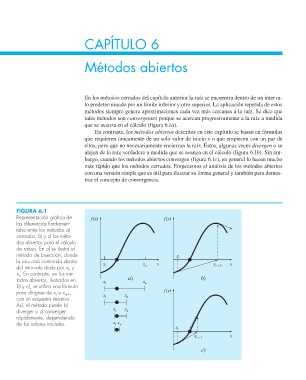
FIGURA 6.1
Representación gráfi ca de f(x) f(x)
las diferencias fundamen-
tales entre los métodos a)
cerrados, b) y c) los méto-
dos abiertos para el cálculo
de raíces. En a) se ilustra el
método de bisección, donde x i
la raíz está contenida dentro
x x x x i + 1 x
del intervalo dado por x l , y l u
x u . En contraste, en los mé-
todos abiertos, ilustrados en x l a) x u b)
b) y c), se utiliza una fórmula
para dirigirse de x i a x i+1 , x x f(x)
con un esquema iterativo. l u
Así, el método puede b)
x x
diverger o c) converger l u
rápidamente, dependiendo
de los valores iniciales. x x u
l
x
i
x i + 1 x
c)

6/12/06 13:49:47
Chapra-06.indd 142 6/12/06 13:49:47
Chapra-06.indd 142