Page 369 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 345

5 10 20 10 10 A

+ +
80 V – 15 25 – 50 V I 1 20 I 2

25 25
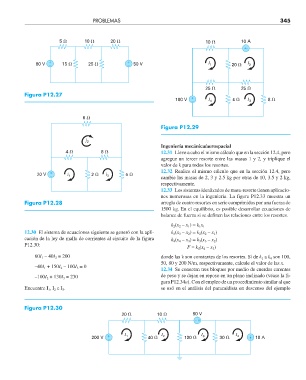
Figura P12.27
100 V + – I 4 4 I 3 8

6
Figura P12.29

j 2
Ingeniería mecánica/aerospacial
4 8 12.31 Lleve a cabo el mismo cálculo que en la sección 12.4, pero
agregue un tercer resorte entre las masas 1 y 2, y triplique el
valor de k para todos los resortes.
20 V – + i 1 2 i 3 5 12.32 Realice el mismo cálculo que en la sección 12.4, pero
cambie las masas de 2, 3 y 2.5 kg por otras de 10, 3.5 y 2 kg,
respectivamente.
12.33 Los sistemas idealizados de masa-resorte tienen aplicacio-
nes numerosas en la ingeniería. La figura P12.33 muestra un
Figura P12.28 arreglo de cuatro resortes en serie comprimidos por una fuerza de
1500 kg. En el equilibrio, es posible desarrollar ecuaciones de
balance de fuerza si se definen las relaciones entre los resortes.

k 2 (x 2 – x 1 ) = k 1 x 1
12.30 El sistema de ecuaciones siguiente se generó con la apli- k 3 (x 3 – x 2 ) = k 2 (x 2 – x 1 )
cación de la ley de malla de corrientes al circuito de la figura k 4 (x 4 – x 3 ) = k 3 (x 3 – x 2 )
P12.30:
F = k 4 (x 4 – x 3 )
60I 1 – 40I 2 = 200 donde las k son constantes de los resortes. Si de k 1 a k 4 son 100,
50, 80 y 200 N/m, respectivamente, calcule el valor de las x.
–40I 1 + 150I 2 – 100I 3 = 0
12.34 Se conectan tres bloques por medio de cuerdas carentes
–100I 2 + 130I 3 = 230 de peso y se dejan en reposo en un plano inclinado (véase la fi-
gura P12.34a). Con el empleo de un procedimiento similar al que
Encuentre I 1 , I 2 e I 3 . se usó en el análisis del paracaidista en descenso del ejemplo

Figura P12.30
20 10 80 V
+ –

+ I 1 I 2 I 3 I 4
200 V 40 100 30 10 A
–

6/12/06 13:54:40
Chapra-12.indd 345 6/12/06 13:54:40
Chapra-12.indd 345