Page 365 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 341

Flujo = F 2

x sal x 2 x 3 x i x i +1 x n –1 x n x ent
1 0 2 ••• 0i ••• n –1 0n
y ent y 1 y 2 y i –1 y i y n –2 y n –1 y sal

Flujo = F 1

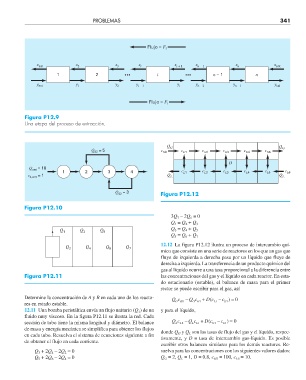
Figura P12.9
Una etapa del proceso de extracción.

Q G Q G
Q 32 = 5 c G0 c G1 c G2 c G3 c G4 c G5
D
Q ent = 10
1 2 3 4 c L1 c L2 c L3 c L4 c L5 c L6
c A,ent = 1 Q L Q L

Q 43 = 3
Figura P12.12

Figura P12.10
3Q 7 – 2Q 6 = 0
Q 1 = Q 2 + Q 3
Q 1 Q 3 Q 5 Q 3 = Q 4 + Q 5
Q 5 = Q 6 + Q 7
12.12 La figura P12.12 ilustra un proceso de intercambio quí-
Q 2 Q 4 Q 6 Q 7
mico que consiste en una serie de reactores en los que un gas que
fluye de izquierda a derecha pasa por un líquido que fluye de
derecha a izquierda. La transferencia de un producto químico del
gas al líquido ocurre a una tasa proporcional a la diferencia entre
Figura P12.11 las concentraciones del gas y el líquido en cada reactor. En esta-
do estacionario (estable), el balance de masa para el primer
rector se puede escribir para el gas, así
Determine la concentración de A y B en cada uno de los reacto- − Qc + =
Qc GG1 D c −( L1 c ) 0
G1
GG0
res en estado estable.
12.11 Una bomba peristáltica envía un flujo unitario (Q 1 ) de un y para el líquido,
fluido muy viscoso. En la figura P12.11 se ilustra la red. Cada
sección de tubo tiene la misma longitud y diámetro. El balance Qc − Qc + D c −( G1 c ) = 0
LL2
LL1
L1
de masa y energía mecánica se simplifica para obtener los flujos
donde Q G y Q L son las tasas de flujo del gas y el líquido, respec-
en cada tubo. Resuelva el sistema de ecuaciones siguiente a fin
tivamente, y D = tasa de intercambio gas-líquido. Es posible
de obtener el flujo en cada corriente.
escribir otros balances similares para los demás reactores. Re-
Q 3 + 2Q 4 – 2Q 2 = 0 suelva para las concentraciones con los siguientes valores dados:
Q 5 + 2Q 6 – 2Q 4 = 0 Q G = 2, Q L = 1, D = 0.8, c G0 = 100, c L6 = 10.
6/12/06 13:54:38
Chapra-12.indd 341
Chapra-12.indd 341 6/12/06 13:54:38