Page 370 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

346 ESTUDIO DE CASOS: ECUACIONES ALGEBRAICAS LINEALES

9.11 se llega al conjunto siguiente de ecuaciones simultáneas (en
x
F la figura P12.34b se muestran los diagramas de cuerpo libre):
100a + T = 519.72
50a – T + R = 216.55
x 4
25a – R = 108.27
k 4 Resuelva para la aceleración a y las tensiones T y R en las dos
cuerdas.
x 3 12.35 Efectúe un cálculo similar al que se utilizó en el problema
k 3 P12.34, pero para el sistema que se ilustra en la figura P12.35.
12.36 Realice el mismo cálculo que en el problema 12.34, pero
x 2 para el sistema que se muestra en la figura P12.36 (los ángulos
son de 45º).
k 2
12.37 Considere el sistema de tres masas y cuatro resortes que
x aparece en la figura P12.37. Al determinar las ecuaciones de
1
movimiento a partir de ∑ F x = ma, para cada masa con el empleo
k
1 de su diagrama de cuerpo libre, se llega a las ecuaciones diferen-
ciales siguientes:
0
⎛ k + k ⎞ ⎛ k ⎞
˙˙ x + 1 2 ⎟ x 1 ⎜ 2 ⎟ x = 0
1 ⎜
–
2
Figura P12.33 ⎝ m 1 ⎠ ⎝ m ⎠
1
⎛ k ⎞ ⎛ k + k ⎞ ⎛ k ⎞
2 ⎜
1 ⎜
x
–
˙˙ – 2 ⎟ x + 2 3 ⎟ x 2 ⎜ 3 ⎟ x = 0
⎝ m ⎠ ⎝ m 2 ⎠ ⎝ m ⎠ 3
2
2
⎛ k ⎞ ⎛ k + k ⎞
3 ⎜
x ˙˙ – 3 ⎟ x + ⎜ 3 4 ⎟ x = 00
⎝ m ⎠ 2 ⎝ m 3 ⎠ 3
3
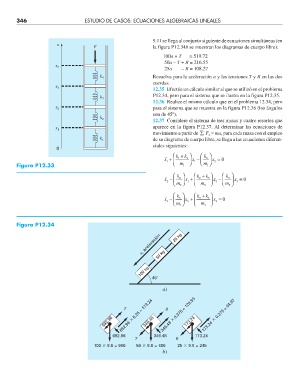
Figura P12.34
a, aceleración 50 kg 25 kg
100 kg
45
a)

692.96 0.25 = 173.24 346.48 0.375 = 129.93 173.24 0.375 = 64.97
T
R
692.96 346.48 173.24

692.96 346.48 173.24
T R
100 9.8 = 980 50 9.8 = 490 25 9.8 = 245
b)

6/12/06 13:54:40
Chapra-12.indd 346
Chapra-12.indd 346 6/12/06 13:54:40