Page 497 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

17.1 REGRESIÓN LINEAL 473

y

x
a)

y

x
b)

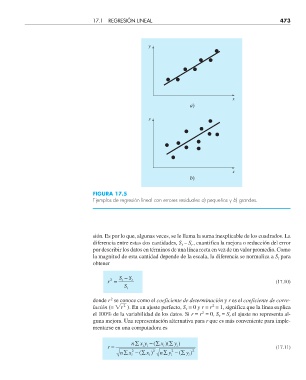
FIGURA 17.5
Ejemplos de regresión lineal con errores residuales a) pequeños y b) grandes.

sión. Es por lo que, algunas veces, se le llama la suma inexplicable de los cuadrados. La
diferencia entre estas dos cantidades, S – S , cuantifica la mejora o reducción del error
r
t
por describir los datos en términos de una línea recta en vez de un valor promedio. Como
la magnitud de esta cantidad depende de la escala, la diferencia se normaliza a S para
t
obtener
S − S
r = t r (17.10)
2
S
t
2
donde r se conoce como el coeficiente de determinación y r es el coeficiente de corre-
—
2
2
lación (= r ). En un ajuste perfecto, S r = 0 y r = r = 1, significa que la línea explica
2
el 100% de la variabilidad de los datos. Si r = r = 0, S r = S t el ajuste no representa al-
guna mejora. Una representación alternativa para r que es más conveniente para imple-
mentarse en una computadora es
n∑ x y − ∑( x )( ∑ y )
r = ii i i (17.11)
n∑ x − ∑( x ) 2 n∑ y − ∑( y ) 2
2
2
i i i i

Chapra-17.indd 473 6/12/06 13:57:14
6/12/06 13:57:14
Chapra-17.indd 473