Page 500 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

476 REGRESIÓN POR MÍNIMOS CUADRADOS

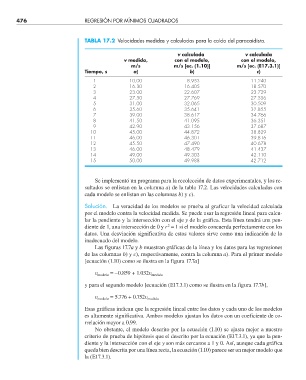
TABLA 17.2 Velocidades medidas y calculadas para la caída del paracaidista.

v calculada v calculada
v medida, con el modelo, con el modelo,
m/s m/s [ec. (1.10)] m/s [ec. (E17.3.1)]
Tiempo, s a) b) c)
1 10.00 8.953 11.240
2 16.30 16.405 18.570
3 23.00 22.607 23.729
4 27.50 27.769 27.556
5 31.00 32.065 30.509
6 35.60 35.641 32.855
7 39.00 38.617 34.766
8 41.50 41.095 36.351
9 42.90 43.156 37.687
10 45.00 44.872 38.829
11 46.00 46.301 39.816
12 45.50 47.490 40.678
13 46.00 48.479 41.437
14 49.00 49.303 42.110
15 50.00 49.988 42.712

Se implementó un programa para la recolección de datos experimentales, y los re-
sultados se enlistan en la columna a) de la tabla 17.2. Las velocidades calculadas con
cada modelo se enlistan en las columnas b) y c).
Solución. La veracidad de los modelos se prueba al graficar la velocidad calculada
por el modelo contra la velocidad medida. Se puede usar la regresión lineal para calcu-
lar la pendiente y la intersección con el eje y de la gráfica. Esta línea tendrá una pen-
2
diente de 1, una intersección de 0 y r = 1 si el modelo concuerda perfectamente con los
datos. Una desviación significativa de estos valores sirve como una indicación de lo
inadecuado del modelo.
Las figuras 17.7a y b muestran gráficas de la línea y los datos para las regresiones
de las columnas b) y c), respectivamente, contra la columna a). Para el primer modelo
[ecuación (1.10) como se ilustra en la figura 17.7a]

v modelo = –0.859 + 1.032v medida

y para el segundo modelo [ecuación (E17.3.1) como se ilustra en la figura 17.7b],
v modelo = 5.776 + 0.752v medida

Esas gráficas indican que la regresión lineal entre los datos y cada uno de los modelos
es altamente significativa. Ambos modelos ajustan los datos con un coeficiente de co-
rrelación mayor a 0.99.
No obstante, el modelo descrito por la ecuación (1.10) se ajusta mejor a nuestro
criterio de prueba de hipótesis que el descrito por la ecuación (E17.3.1), ya que la pen-
diente y la intersección con el eje y son más cercanos a 1 y 0. Así, aunque cada gráfica
queda bien descrita por una línea recta, la ecuación (1.10) parece ser un mejor modelo que
la (E17.3.1).

6/12/06 13:57:14
Chapra-17.indd 476 6/12/06 13:57:14
Chapra-17.indd 476