Page 547 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

18.5 COMENTARIOS ADICIONALES 523

computadoras digitales, dichas técnicas tenían gran utilidad para interpolación a partir
de tablas con datos igualmente espaciados. De hecho, se desarrolló una estructura compu-
tacional, conocida como tabla de diferencias divididas, para facilitar la implementación
de dichas técnicas. (La figura 18.5 es un ejemplo de esa tabla.)
Sin embargo, como las fórmulas dadas son subconjuntos de los esquemas de Newton
y Lagrange compatibles con una computadora y debido a las muchas funciones tabulares
existentes, como subrutinas de bibliotecas, ha disminuido la necesidad de tener versiones
para datos igualmente espaciados. A pesar de ello, las hemos incluido en este tema por
su relevancia en las últimas partes de este libro. En especial, son necesarias para obtener
fórmulas de integración numérica que por lo común utilizan datos igualmente espaciados
(capítulo 21). Como las fórmulas de integración numérica son importantes en la solución
de ecuaciones diferenciales ordinarias, el análisis del cuadro 18.2 adquiere también
significado para la parte siete.
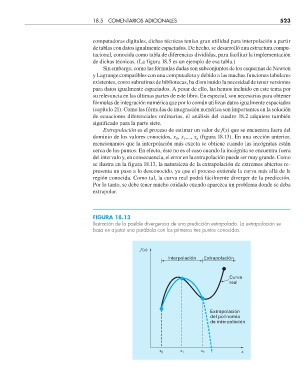
Extrapolación es el proceso de estimar un valor de f(x) que se encuentra fuera del
dominio de los valores conocidos, x , x ,..., x (figura 18.13). En una sección anterior,
0
1
n
mencionamos que la interpolación más exacta se obtiene cuando las incógnitas están
cerca de los puntos. En efecto, éste no es el caso cuando la incógnita se encuentra fuera
del intervalo y, en consecuencia, el error en la extrapolación puede ser muy grande. Como
se ilustra en la figura 18.13, la naturaleza de la extrapolación de extremos abiertos re-
presenta un paso a lo desconocido, ya que el proceso extiende la curva más allá de la
región conocida. Como tal, la curva real podrá fácilmente diverger de la predicción.
Por lo tanto, se debe tener mucho cuidado cuando aparezca un problema donde se deba
extrapolar.

FIGURA 18.13
Ilustración de la posible divergencia de una predicción extrapolada. La extrapolación se
basa en ajustar una parábola con los primeros tres puntos conocidos.

f (x)
Interpolación Extrapolación

Curva
real

Extrapolación
del polinomio
de interpolación

x 0 x 1 x 2 x

6/12/06 13:57:53
Chapra-18.indd 523 6/12/06 13:57:53
Chapra-18.indd 523