Page 554 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

530 INTERPOLACIÓN

f(x) a x + b x + c 3
2
3
3
2
a x + b x + c 2 f(x )
2
2
2
a x + b x + c 1 3
1
1
f(x )
1
f(x ) f(x )
0
2
Intervalo 1 Intervalo 2 Intervalo 3
x 0 x 1 x 2 x 3 x
i =0 i =1 i =2 i =3

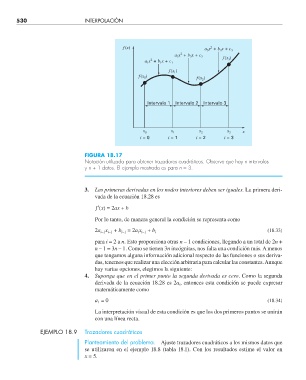
FIGURA 18.17
Notación utilizada para obtener trazadores cuadráticos. Observe que hay n intervalos
y n + 1 datos. El ejemplo mostrado es para n = 3.

3. Las primeras derivadas en los nodos interiores deben ser iguales. La primera deri-
vada de la ecuación 18.28 es

ƒ′(x) = 2ax + b
Por lo tanto, de manera general la condición se representa como

2a x + b = 2a x + b i (18.33)
i i–1
i–1
i–1 i–1
para i = 2 a n. Esto proporciona otras n – 1 condiciones, llegando a un total de 2n +
n – 1 = 3n – 1. Como se tienen 3n incógnitas, nos falta una condición más. A menos
que tengamos alguna información adicional respecto de las funciones o sus deriva-
das, tenemos que realizar una elección arbitraria para calcular las constantes. Aunque
hay varias opciones, elegimos la siguiente:
4. Suponga que en el primer punto la segunda derivada es cero. Como la segunda
derivada de la ecuación 18.28 es 2a , entonces esta condición se puede expresar
i
matemáticamente como
a = 0 (18.34)
1
La interpretación visual de esta condición es que los dos primeros puntos se unirán
con una línea recta.

EJEMPLO 18.9 Trazadores cuadráticos
Planteamiento del problema. Ajuste trazadores cuadráticos a los mismos datos que
se utilizaron en el ejemplo 18.8 (tabla 18.1). Con los resultados estime el valor en
x = 5.

6/12/06 13:57:55
Chapra-18.indd 530 6/12/06 13:57:55
Chapra-18.indd 530