Page 573 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

19.2 SERIE DE FOURIER CONTINUA 549

De manera similar, se determina que todas las b = 0. Entonces, la aproximación de la
serie de Fourier es
ft( ) = 4 cos(ω t) − 4 cos(3ω t) + 4 cos(5ω t) − 4 cos(7ω t) +
π 0 3π 0 5π 0 7π 0

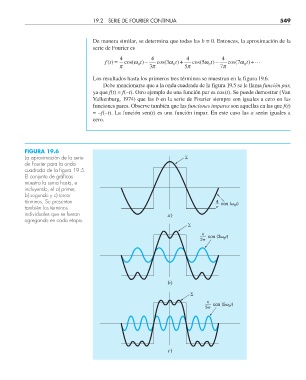
Los resultados hasta los primeros tres términos se muestran en la figura 19.6.
Debe mencionarse que a la onda cuadrada de la figura 19.5 se le llama función par,
ya que f(t) = f(–t). Otro ejemplo de una función par es cos(t). Se puede demostrar (Van
Valkenburg, 1974) que las b en la serie de Fourier siempre son iguales a cero en las
funciones pares. Observe también que las funciones impares son aquellas en las que f(t)
= –f(–t). La función sen(t) es una función impar. En este caso las a serán iguales a
cero.

FIGURA 19.6
La aproximación de la serie
de Fourier para la onda
cuadrada de la fi gura 19.5.
El conjunto de gráfi cas
muestra la suma hasta, e
incluyendo, el a) primer,
b) segundo y c) tercer
términos. Se presentan 4 cos ( t)
también los términos 0
individuales que se fueron a)
agregando en cada etapa.

4
cos (3 t)
3 0

b)

4
cos (5 t)
5 0

c)

6/12/06 13:58:22
Chapra-19.indd 549
Chapra-19.indd 549 6/12/06 13:58:22