Page 572 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

548 APROXIMACIÓN DE FOURIER

para k = 1, 2,… y

a = 1 ∫ T ft dt() (19.20)
0
T 0

EJEMPLO 19.2 Aproximación de la serie de Fourier continua

Planteamiento del problema. Utilice la serie de Fourier continua para aproximar la
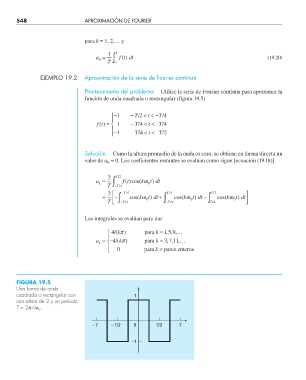
función de onda cuadrada o rectangular (figura 19.5)

⎧ −1 − T/ < < − T/4
2
t
⎪
4
t
ft() = ⎨ 1 − T/ < < T/4
⎪
⎩ −1 T/ < < T/2
t
4
Solución. Como la altura promedio de la onda es cero, se obtiene en forma directa un
valor de a = 0. Los coeficientes restantes se evalúan como sigue [ecuación (19.18)]
0
2 T 2 /
a = ∫ ft( )cos( kω t dt)
k
T − T 2 / 0
2 ⎡ − T 4 / T 4 / T 2 / ⎤
−
= ⎢ ∫ cos( kω t dt +) ∫ cos( kω t dt −) ∫ cos( kω t dt)
T ⎣ − T 2 / 0 − T 4 / 0 T 4 0 ⎥ ⎦
/
Las integrales se evalúan para dar

⎧ 4/( k ) π para k = 1 5 9, , , …
⎪
a = −4/( π para k = 3 7 11, , , …
⎨
k )
k
⎪
⎩ 0 para k = pares enteros

FIGURA 19.5
Una forma de onda
cuadrada o rectangular con 1
una altura de 2 y un periodo
T = 2p/w 0 .

–T –T/2 0 T/2 T

–1

6/12/06 13:58:22
Chapra-19.indd 548 6/12/06 13:58:22
Chapra-19.indd 548