Page 75 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 51

inicio
II I
y
m = n – 1 r

x

cambio = falso

III IV
T i = 1
i > m
i = i + 1
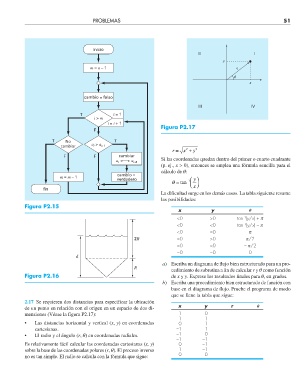
Figura P2.17
F
T No T
cambiar a i > a i+1
r = x + y 2
2
F F cambiar
Si las coordenadas quedan dentro del primer o cuarto cuadrante
a i a i+1
(p. ej., x > 0), entonces se emplea una fórmula sencilla para el
cálculo de q:
cambio =
m = m – 1
verdadero ⎛ ⎞ y
θ = tan –1
⎝ ⎠ x
fin
La dificultad surge en los demás casos. La tabla siguiente resume
las posibilidades:
Figura P2.15
x y θ
<0 >0 tan (y/x) + p
–1
<0 <0 tan (y/x) – p
–1
<0 =0 p
2R =0 >0 p/2
=0 <0 – p/2
=0 =0 0
d
a) Escriba un diagrama de fl ujo bien estructurado para un pro-
R
cedimiento de subrutina a fi n de calcular r y q como función
Figura P2.16 de x y y. Exprese los resultados fi nales para q, en grados.
b) Escriba una procedimiento bien estructurado de función con
base en el diagrama de fl ujo. Pruebe el programa de modo
que se llene la tabla que sigue:
2.17 Se requieren dos distancias para especificar la ubicación
x y r θ
de un punto en relación con el origen en un espacio de dos di-
mensiones (Véase la figura P2.17): 1 0
1 1
• Las distancias horizontal y vertical (x, y) en coordenadas 0 1
cartesianas. –1 1
• El radio y el ángulo (r, q) en coordenadas radiales. –1 0
–1 –1
Es relativamente fácil calcular las coordenadas cartesianas (x, y) 0 –1
sobre la base de las coordenadas polares (r, q). El proceso inverso 1 –1
0 0
no es tan simple. El radio se calcula con la fórmula que sigue:

6/12/06 13:43:47
Chapra-02.indd 51 6/12/06 13:43:47
Chapra-02.indd 51