Page 857 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

28.2 MODELOS DEPREDADOR-PRESA Y CAOS 833

c

10

5

0
0 10 20 t

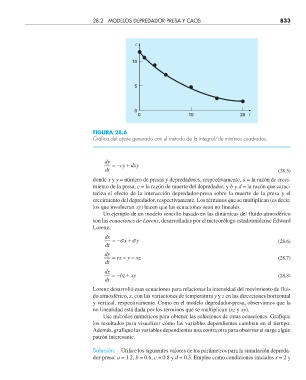
FIGURA 28.6
Gráfi ca del ajuste generado con el método de la integral/de mínimos cuadrados.

dy
=− cy dxy+
dt (28.5)
donde x y y = número de presas y depredadores, respectivamente, a = la razón de creci-
miento de la presa, c = la razón de muerte del depredador, y b y d = la razón que carac-
teriza el efecto de la interacción depredador-presa sobre la muerte de la presa y el
crecimiento del depredador, respectivamente. Los términos que se multiplican (es decir,
los que involucran xy) hacen que las ecuaciones sean no lineales.
Un ejemplo de un modelo sencillo basado en las dinámicas del fluido atmosférico
son las ecuaciones de Lorenz, desarrolladas por el meteorólogo estadounidense Edward
Lorenz,
dx
=−σ x + σ y (28.6)
dt
dy
= rx − − xz (28.7)
y
dt
dz
=− bz + xy (28.8)
dt
Lorenz desarrolló esas ecuaciones para relacionar la intensidad del movimiento de flui-
do atmosférico, x, con las variaciones de temperatura y y z en las direcciones horizontal
y vertical, respectivamente. Como en el modelo depredador-presa, observamos que la
no linealidad está dada por los términos que se multiplican (xz y xy).
Use métodos numéricos para obtener las soluciones de estas ecuaciones. Grafique
los resultados para visualizar cómo las variables dependientes cambian en el tiempo.
Además, grafique las variables dependientes una contra otra para observar si surge algún
patrón interesante.

Solución. Utilice los siguientes valores de los parámetros para la simulación depreda-
dor-presa: a = 1.2, b = 0.6, c = 0.8 y d = 0.3. Emplee como condiciones iniciales x = 2 y

6/12/06 14:03:37
Chapra-28.indd 833 6/12/06 14:03:37
Chapra-28.indd 833