Page 860 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

836 ESTUDIO DE CASOS: ECUACIONES DIFERENCIALES ORDINARIAS

aleatorio de oscilaciones, rebotando de valores negativos a positivos. Sin embargo, aun
cuando los patrones parezcan aleatorios, la frecuencia de la oscilación y las amplitudes
parecen bastante consistentes.
Otra característica interesante se puede ilustrar cambiando ligeramente la condición
inicial de x (de 5 a 5.001). Los resultados están superpuestos como una línea punteada
en la figura 28.9. Aunque las soluciones siguen un mismo comportamiento por un tiem-
po, después de aproximadamente t = 12.5 divergen significativamente. Así, se observa
que las ecuaciones de Lorenz son muy sensibles a las condiciones iniciales. En su estu-
dio original, esto llevó a Lorenz a la conclusión de que ¡pronosticar el clima a largo
plazo será imposible!
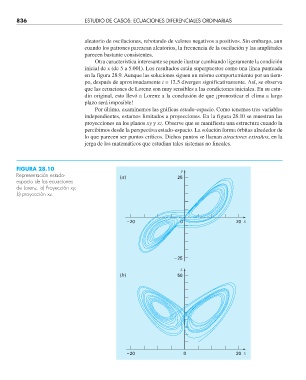
Por último, examinemos las gráficas estado-espacio. Como tenemos tres variables
independientes, estamos limitados a proyecciones. En la figura 28.10 se muestran las
proyecciones en los planos xy y xz. Observe que se manifiesta una estructura cuando la
percibimos desde la perspectiva estado-espacio. La solución forma órbitas alrededor de
lo que parecen ser puntos críticos. Dichos puntos se llaman atractores extraños, en la
jerga de los matemáticos que estudian tales sistemas no lineales.

FIGURA 28.10 y
Representación estado- (a) 25
espacio de las ecuaciones
de Lorenz. a) Proyección xy;
b) proyección xz.

–20 0 20 x

–25
z
(b) 50

–20 0 20 x

6/12/06 14:03:38
Chapra-28.indd 836
Chapra-28.indd 836 6/12/06 14:03:38