Page 247 - Applied Statistics with R

12.4. POST HOC TESTING 247

going to perform 100 -tests. Suppose you wish to do this with a false positive
rate of = 0.05. If we use this significance level for each test, for 100 tests,
we then expect 5 false positives. That means, with 100 tests, we’re almost
guaranteed to have at least one error.
What we’d really like, is for the family-wise error rate to be 0.05. If we consider
the 100 tests to be a single “experiment” the FWER is the rate of one or more
false positives for in the full experiment (100 tests). Consider it an error rate
for an entire procedure, instead of a single test.
With this in mind, one of the simplest adjustments we can make, is to increase
the p-values for each test, depending on the number of tests. In particular the
Bonferroni correction simply multiplies by the number of tests.

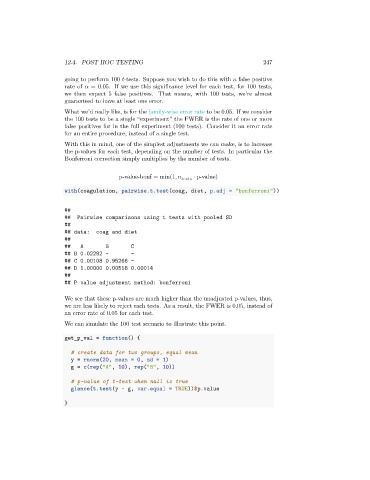
p-value-bonf = min(1, ⋅ p-value)

with(coagulation, pairwise.t.test(coag, diet, p.adj = "bonferroni"))

##
## Pairwise comparisons using t tests with pooled SD
##
## data: coag and diet
##
## A B C
## B 0.02282 - -
## C 0.00108 0.95266 -
## D 1.00000 0.00518 0.00014
##
## P value adjustment method: bonferroni

We see that these p-values are much higher than the unadjusted p-values, thus,
we are less likely to reject each tests. As a result, the FWER is 0.05, instead of
an error rate of 0.05 for each test.
We can simulate the 100 test scenario to illustrate this point.

get_p_val = function() {

# create data for two groups, equal mean
y = rnorm(20, mean = 0, sd = 1)
g = c(rep("A", 10), rep("B", 10))

# p-value of t-test when null is true
glance(t.test(y ~ g, var.equal = TRUE))$p.value
}